摘要:(2)当S20.即a1=a2=1.S2=2或a1=a2=-1.S2=-2.
网址:http://m.1010jiajiao.com/timu_id_447305[举报]
已知问题“设正数x,y满足
+
=1,求x+y的最值”有如下解法;
设
=cos2α,
=sin2α,α∈(0,
),
则x=sec2α=1+tan2α,y=2csc2α=2(1+cot2α),
所以,x+y=3+tan2α+2cot2α=3+tan2+
≥3+2
,等号成立当且仅当tan2α=
,即tan2α=
,此时x=1+
,y=2+
.
(1)参考上述解法,求函数y=
+2
的最大值.
(2)求函数y=2
-
(x≥0)的最小值.
查看习题详情和答案>>
| 1 |
| x |
| 2 |
| y |
设
| 1 |
| x |
| 2 |
| y |
| π |
| 2 |
则x=sec2α=1+tan2α,y=2csc2α=2(1+cot2α),
所以,x+y=3+tan2α+2cot2α=3+tan2+
| 2 |
| tan2α |
| 2 |
| 2 |
| tan2α |
| 2 |
| 2 |
| 2 |
(1)参考上述解法,求函数y=
| 1-x |
| x |
(2)求函数y=2
| x+1 |
| x |
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

【解析】本题主要考查函数的应用,导数及均值不等式的应用等,考查学生分析问题和解决问题的能力 第一问要利用相似比得到结论。
(I)由SAMPN > 32 得 > 32 ,
> 32 ,
∵x >2,∴ ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴2<X<8/3,即AN长的取值范围是(2,8/3)或(8,+ )
)
第二问, 
当且仅当
(3)令
∴当x
> 4,y′> 0,即函数y= 在(4,+∞)上单调递增,∴函数y=
在(4,+∞)上单调递增,∴函数y= 在[6,+∞]上也单调递增.
在[6,+∞]上也单调递增.
∴当x=6时y= 取得最小值,即SAMPN取得最小值27(平方米).
取得最小值,即SAMPN取得最小值27(平方米).
查看习题详情和答案>>
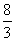 B.3+2
B.3+2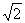 C.6
D.9
C.6
D.9