摘要:例1.在研究小车速度随时间变化规律的实验中.按照实验进行的先后顺序.将下列步骤的代号填在横线上 DBFAEGC . A. 把穿过打点计时器的纸带固定在小车后面. B. 把打点计时器固定在木板没有滑轮的一端.并连好电路. C. 换上新的纸带.再重做两次. D. 把长木板平放在实验桌上.并使滑轮伸出桌面. E. 使小车停在靠近打点计时器处.接通电源.放开小车.让小车运动. F. 把一条细绳拴在小车上.细绳跨过定滑轮.下边吊着合适的钩码. G. 断开电源.取出纸带. 例2.在实验中.算出小车经过各计数点的瞬时速度如下表. 计数点序号 1 2 3 4 5 6 计数点对应的时刻(s) 0.10 0.20 0.30 0.40 0.50 0.60 通过计数点的速度 44.0 62.0 81.0 100.0 110.0 168.0 为了计算加速度.合理的方法是(C ) A. 根据任意两点的速度用公式算出加速度. B. 根据实验数据画出速度-时间图象.量出其倾角.同公式求出加速度 C. 根据实验数据画出速度-时间图象.由图象上相距较远的两点所对应的速度.时间用公式算出加速度. D. 依次算出通过连续两计数点间的加速度.算出平均值作为小车的加速度. 解析:方法A偶然误差较大.方法D实际也是仅由始末两个速度决定.偶然误差也较大.只有利用实验数据画出对应的速度-时间图象.才可充分利用各次测量数据.减小偶然误差.由于在物理图象上.两坐标轴的分度大小往往是不相等的.不同的坐标分度会得到不同的倾角.当然的值也不一样.所以B错,C正确. 扩展:其实除了作速度时间图象能充分利用实验所有数据.减小偶然误差外.还有一种方法也能做到这一点.就是在D选项上稍加修改:依次算出通过连续两计数点间的加速度.但取点不能重复.比如第一次取1.2两点.第二次就取3.4两点.第三次取5.6两点.依次类推--.但总的来说还是图象法好一点.直观.用图象法还可以很容易找出偏离函数图象太远的误差较大的点.
网址:http://m.1010jiajiao.com/timu_id_4470768[举报]
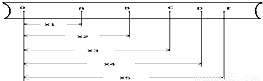
在研究小车速度随时间变化规律的实验中,得到一条记录小车运动情况的点迹清晰的纸带,如图3-2-6所示,图中A、B、C、D、E为相邻计数点,相邻计数点的时间间隔T=0.1 s.
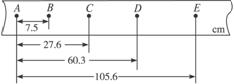
图3-2-6
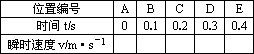
(1)根据纸带上的数据,计算各点速度,填入下表中.
位置编号 | A | B | C | D | E |
时间t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
瞬时速度v/(m·s-1) |
|
|
|
|
|
(2)在图3-2-7中作出小车的v-t图线.

图3-2-7
查看习题详情和答案>>在研究小车速度随时间变化规律的实验中,得到一条记录小车运动情况的点迹清晰的纸带,如图(a)所示,图中A、B、C、D、E为相邻计数点,相邻计数点的时间间隔T=0.1 s.
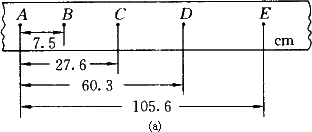
(1)根据纸带上的数据,计算各点的速度,填入下表中.
(2)在图(b)中做出小车的v-t图线.
在“探究小车速度随时间变化规律”的实验中:
(1)下列操作正确的有
A、在释放小车前,小车要靠近打点计时器B、打点计时器应放在长木板的有滑轮一端C、应先接通电源,后释放小车D、电火花计时器应使用低压交流电源
(2)打点计时器原来使用的电源的频率是50Hz,若在测定匀变速直线运动的加速度时,
交流电的频率为60Hz而未被发觉,这样计算出的加速度值与真实值相比是
(3)某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示.在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为s1、s2和s3.由此可算出小车运动的加速度大小a=
,打点计时器在打C点时,小车的速度大小
.(用已知的物理量符号表示)

查看习题详情和答案>>
(1)下列操作正确的有
AC
AC
.(填选项代号)A、在释放小车前,小车要靠近打点计时器B、打点计时器应放在长木板的有滑轮一端C、应先接通电源,后释放小车D、电火花计时器应使用低压交流电源
(2)打点计时器原来使用的电源的频率是50Hz,若在测定匀变速直线运动的加速度时,
交流电的频率为60Hz而未被发觉,这样计算出的加速度值与真实值相比是
偏小
偏小
.(填“偏大”、“偏小”或“不变”)(3)某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示.在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为s1、s2和s3.由此可算出小车运动的加速度大小a=
| s3-s2-s1 |
| 2T2 |
| s3-s2-s1 |
| 2T2 |
| s3-s1 |
| 2T |
| s3-s1 |
| 2T |

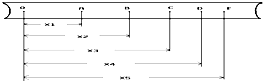 在“研究小车速度随时间变化的规律”实验中,用打点计时器记录纸带运动时间.打点计时器接在50Hz的交流电源上.如图所示为做直线运动的小车带动纸带记录的5个计数点,每相邻两个计数点间都有4个点未画出.用刻度尺测出计数点A、B、C、D、E到O点的距离为x1=8.78cm、x2=16.08cm、x3=21.87cm、x4=26.16cm、x5=28.94cm.由上面的数据分析,小车的运动是
在“研究小车速度随时间变化的规律”实验中,用打点计时器记录纸带运动时间.打点计时器接在50Hz的交流电源上.如图所示为做直线运动的小车带动纸带记录的5个计数点,每相邻两个计数点间都有4个点未画出.用刻度尺测出计数点A、B、C、D、E到O点的距离为x1=8.78cm、x2=16.08cm、x3=21.87cm、x4=26.16cm、x5=28.94cm.由上面的数据分析,小车的运动是