网址:http://m.1010jiajiao.com/timu_id_4468312[举报]
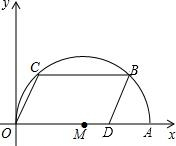 (2013•长宁区一模)在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
(2013•长宁区一模)在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.(1)求C点坐标;
(2)求过O、C、B三点的抛物线解析式,并用配方法求出该抛物线的顶点坐标和对称轴;
(3)判断:(2)中抛物线的顶点与⊙M的位置关系,说明理由.
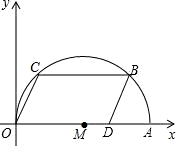 在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
(1)求C点坐标;
(2)求过O、C、B三点的抛物线解析式,并用配方法求出该抛物线的顶点坐标和对称轴;
(3)判断:(2)中抛物线的顶点与⊙M的位置关系,说明理由.
查看习题详情和答案>>
(1)求C点坐标;
(2)求过O、C、B三点的抛物线解析式,并用配方法求出该抛物线的顶点坐标和对称轴;
(3)判断:(2)中抛物线的顶点与⊙M的位置关系,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
在同一直角坐标系中作出函数y=-2x2,y=-2(x-2)2和y=-2(x+3)2的图象,然后根据图象填空:

抛物线y=-2x2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=-2(x-2)2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=-2(x+3)2的顶点坐标是( ),对称轴是________,开口向________.
可以发现,抛物线y=-2(x-2)2,y=-2(x+3)2与抛物线y=-2x2的形状、开口大小相同,只是抛物线的位置和对称轴发生了变化.把抛物线y=-2x2沿x轴向________平移________个单位即可得到抛物线y=-2(x-2)2;把抛物线y=-2x2沿x轴向________平移________个单位即可得到抛物线y=-2(x+3)2.
一般地,抛物线y=a(x+m)2的顶点坐标是( ),对称轴是________.
查看习题详情和答案>>在同一直角坐标系中作出函数y=x2,y=(x-2)2和y=(x-2)2+3的图象,然后根据图象填空:

抛物线y=x2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=(x-2)2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=(x-2)2+3的顶点坐标是( ),对称轴是________,开口向________.
可以发现,抛物线y=(x-2)2,y=(x-2)2+3与抛物线y=x2的形状、开口大小相同,只是抛物线的位置发生了变化.把抛物线y=x2沿x轴向________平移________个单位即可得到抛物线y=(x-2)2;把抛物线y=(x-2)2沿y轴向________平移________个单位即可得到抛物线y=(x-2)2+3;也就是说,把抛物线y=x2沿x轴向________平移________个单位,再沿y轴向________平移________个单位即可得到抛物线y=(x-2)2+3.
还可以发现,对于y=x2,当x<0时y的值随x值的增大而________,当x>0时y的值随x值的增大而________;对于y=k(x-2)2,当x<2时,y的值随x值的增大而________,当x>2时,y的值随x值的增大而________;对于y=(x-2)2+3,当x<2时,y的值随x值的增大而________,当x>2时,y的值随x值的增大而________.
查看习题详情和答案>>