题目内容
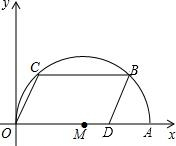 (2013•长宁区一模)在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
(2013•长宁区一模)在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.(1)求C点坐标;
(2)求过O、C、B三点的抛物线解析式,并用配方法求出该抛物线的顶点坐标和对称轴;
(3)判断:(2)中抛物线的顶点与⊙M的位置关系,说明理由.
分析:(1)作MN⊥BC于点N,连接MC,利用垂径定理求得线段MN后即可确定点C的坐标;
(2)用同样的方法确定点D的坐标后利用待定系数法确定二次函数的解析式,然后配方后即可确定抛物线的顶点坐标及对称轴;
(3)根据抛物线的顶点坐标和点M的坐标确定两点之间的距离,然后根据半径与两点之间的线段的大小关系即可确定顶点与圆的位置关系.
(2)用同样的方法确定点D的坐标后利用待定系数法确定二次函数的解析式,然后配方后即可确定抛物线的顶点坐标及对称轴;
(3)根据抛物线的顶点坐标和点M的坐标确定两点之间的距离,然后根据半径与两点之间的线段的大小关系即可确定顶点与圆的位置关系.
解答: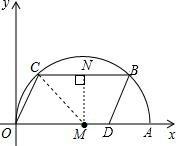 解:(1)如图,作MN⊥BC于点N,连接MC,
解:(1)如图,作MN⊥BC于点N,连接MC,
∵A(10,0)和点D(8,0).
∴点M(5,0),
∵点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形,
∴⊙M的半径为5,BC=OD=8,
∴在Rt△MNC中,MC=5,NC=
BC=4,
∴MN=3,
∴点C的坐标为(1,3);
(2)∵点C的坐标为(1,3),
∴点B的坐标为(9,3),
设过O、C、B三点的抛物线解析式为y=ax2+bx,
∴
解得:
∴解析式为:y=-
x2+
x,
∴y=-
x2+
x=-
(x-5)2+
,
∴对称轴为x=5,顶点坐标为(5,
);
(3)∵顶点坐标为(5,
),点M的坐标为(5,0),
∴顶点到点M的距离为
,
∵
>5
∴抛物线的顶点在⊙M外.
 解:(1)如图,作MN⊥BC于点N,连接MC,
解:(1)如图,作MN⊥BC于点N,连接MC,∵A(10,0)和点D(8,0).
∴点M(5,0),
∵点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形,
∴⊙M的半径为5,BC=OD=8,
∴在Rt△MNC中,MC=5,NC=
| 1 |
| 2 |
∴MN=3,
∴点C的坐标为(1,3);
(2)∵点C的坐标为(1,3),
∴点B的坐标为(9,3),
设过O、C、B三点的抛物线解析式为y=ax2+bx,
∴
|
解得:
|
∴解析式为:y=-
| 1 |
| 3 |
| 10 |
| 3 |
∴y=-
| 1 |
| 3 |
| 10 |
| 3 |
| 1 |
| 3 |
| 25 |
| 3 |
∴对称轴为x=5,顶点坐标为(5,
| ,25 |
| 3 |
(3)∵顶点坐标为(5,
| ,25 |
| 3 |
∴顶点到点M的距离为
| 25 |
| 3 |
∵
| 25 |
| 3 |
∴抛物线的顶点在⊙M外.
点评:本题考查了二次函数的综合知识,还考查了点与圆的位置关系,本题难度不大,但综合性比较强.

练习册系列答案
相关题目
 (2013•长宁区一模)如图,圆O的弦AB垂直平分半径OC,则四边形OACB一定是( )
(2013•长宁区一模)如图,圆O的弦AB垂直平分半径OC,则四边形OACB一定是( )