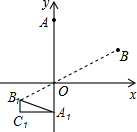（2006•福州质检）如图，直角三角形A₁B₁C₁中，∠C₁=90°，点A、A₁在y轴上，且AO=2A₁O，连接B₁O并延长至B，使BO=2B₁O，请用尺规完成下列作图：连接C₁O并延长至C，使CO=2C₁O，连接AB、BC、CA，则△A₁B₁C₁△ABC（填≌或∽），若∠B₁A₁C₁=30°，A₁（0，-1.5），C₁（-

3

，-1.5），则△ABC中，边AB的长是．

实验与探究：在△ABC中，∠A、∠B、∠C所对应的边分别用a、b、c表示．

（1）如图1，在△ABC中，∠A=2∠B，且∠A=60°．易证：a²=b（b+c）
（2）如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．本题第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角△ABC，如图2，∠A=2∠B，关系式a²=b（b+c）是否仍然成立？并证明你的结论．
归纳与发现
由以上的证明，可以得到关于倍角三角形的一个结论：一个三角形中有一个角等于另一个角的两倍，2倍角所对边的平方等于一倍角所对边乘该边与第三边的和．
运用与推广
（3）（2009年全国初中数学联赛）在△ABC中，最大角∠A是最小角∠C的2倍，且AB=7，AC=8．则BC=
（A）7

2

   （B）10   （C）

105

    （D）7

3

（4）是否存在一个三边长恰是三个连续正整数，且其中一个内角等于另一个内角2倍的△ABC？证明你的结论．