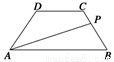
摘要:等腰梯形ABCD的两底分别为AB=10.CD=4.两腰AD=CB=5.动点P由B点沿折线BCDA向A运动.设P点所经过的路程为x.三角形ABP的面积为S. 的解析式, (2)试确定点P的位置.使△ABP的面积S最大. 解 (1)过C点作CE⊥AB于E. 在△BEC中.CE==4.∴sinB=. 由题意.当x∈(0.5]时.过P点作PF⊥AB于F. ∴PF=xsinB=x.∴S=×10×x=4x, 当x∈(5.9]时.∴S=×10×4=20. 当x∈(9.14]时.AP=14-x.PF=AP·sinA=. ∴S=×10× ×=56-4x.综上可知,函数S=f(x)= 知,当x∈=4x为增函数, 所以,当x=5时,取得最大值20. 当x∈=20,最大值为20. 当x∈=56-4x为减函数,无最大值. 综上可知:当P点在CD上时,△ABP的面积S最大为20.
网址:http://m.1010jiajiao.com/timu_id_4463573[举报]
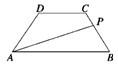 等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大. 查看习题详情和答案>>
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.
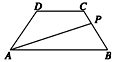
等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)试确定点P的位置,使△ABP的面积S最大.