摘要：某工厂生产某种产品.已知该产品的月生产量x(t)与1 t产品的价格p之间的关系为: p=24 200-x2.且生产x t的成本为R(元).其中R=50 000+200x.问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少? 解 每月生产x t时的利润为 f(x)=(24 200-x2)x-=-x3+24 000x-50 000 . 由=-x2+24 000=0, 解得x1=200,x2=-200. 因f内只有一个极值点x=200且为极大值.故它就是最大值点.且最大值为 f(200)=-(200)3+24 000×200-50 000=3 150 000(元). 故该厂每月生产200吨产品才能使利润达到最大且最大利润为3 150 000元. ? 单元检测二
网址：http://m.1010jiajiao.com/timu_id_4463555[举报]
某工厂生产某种产品，已知该产品的产量x（吨）与每吨产品的价格P（元/吨）之间的关系为P=24200-
x2，且生产x吨的成本为R=50000+200x元．问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入-成本）
查看习题详情和答案>>
| 1 | 5 |
某工厂生产某种产品，已知该产品的月生产量x（吨）与每吨产品的价格P（元/吨）之间的关系式为P=24200-
x2，且生产x吨的成本为R=50000+200x（元）．
（1）求该工厂月利润L（元）关于月生产量x（吨）的函数关系式；（月利润=月收入-月成本）
（2）求该工厂每月生产多少吨产品才能使月利润达到最大？并求出最大利润．
查看习题详情和答案>>
| 1 | 5 |
（1）求该工厂月利润L（元）关于月生产量x（吨）的函数关系式；（月利润=月收入-月成本）
（2）求该工厂每月生产多少吨产品才能使月利润达到最大？并求出最大利润．
某工厂生产某种产品，已知该产品每吨的价格P（元）与产量x（吨）之间的关系式为 P=24200-
x2，且生产x吨的成本为（50000+200x）元，则该厂利润最大时，生产的产品的吨数为
查看习题详情和答案>>
| 1 | 5 |
200
200
．
x2，且生产xt的成本为R（元），其中R=50 000+200x.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入-成本）
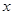（吨）与每吨产品的价格
（元/吨）之间的关系式为：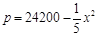
,且生产x吨的成本为
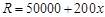（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）