摘要:已知函数f(x)=x2+|x-a|+1,a∈R. 的奇偶性, (2)若-≤a≤.求f(x)的最小值. 解 =(-x)2+|-x|+1=f(x), 此时,f(x)为偶函数.当a≠0时.f(a)=a2+1,f(-a)=a2+2|a|+1, f≠-f 为非奇非偶函数. =x2-x+a+1=(x-)2+a+, ∵a≤,故函数f(x)在(-∞.a]上单调递减. 从而函数f(x)在(-∞.a]上的最小值为f(a)=a2+1. 当x≥a时.函数f(x)=x2+x-a+1=(x+)2-a+, ∵a≥-.故函数f上单调递增.从而函数f上的最小值为f(a)=a2+1. 综上得.当-≤a≤时.函数f(x)的最小值为a2+1.
网址:http://m.1010jiajiao.com/timu_id_4463452[举报]
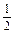 ≤a≤
≤a≤