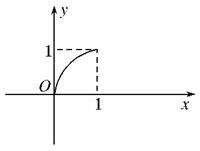
摘要:已知定义在区间满足f(=f(x1)-f(x2).且当x>1时.f(x)<0. 的值, 的单调性, =-1,解不等式f(|x|)<-2. 解 (1)令x1=x2>0, 代入得f(1)=f(x1)-f(x1)=0,故f(1)=0. (2)任取x1,x2∈.且x1>x2,则>1, 由于当x>1时.f(x)<0, 所以f<0,即f(x1)-f(x2)<0, 因此f(x1)<f(x2), 所以函数f上是单调递减函数. (3)由f=f(x1)-f(x2)得 f=f=-1,所以f(9)=-2. 由于函数f上是单调递减函数. 由f,得|x|>9,∴x>9或x<-9.因此不等式的解集为{x|x>9或x<-9}.
网址:http://m.1010jiajiao.com/timu_id_4463421[举报]
已知定义在区间[0, ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
A.
B.
C.
D.3π
查看习题详情和答案>>
 ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )A.

B.

C.

D.3π
查看习题详情和答案>>
已知定义在区间[0, ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x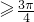 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为
- A.
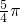
- B.

- C.

- D.3π
已知定义在区间[-p,![]() ] 上的函数y=f(x)的图象关于直线x= -
] 上的函数y=f(x)的图象关于直线x= -![]() 对称,当xÎ[-
对称,当xÎ[-![]() ,
,![]() ]时,函数f(x)=Asin(wx+j)(A>0, w>0,-
]时,函数f(x)=Asin(wx+j)(A>0, w>0,-![]() <j<
<j<![]() ),其图象如图所示。
),其图象如图所示。
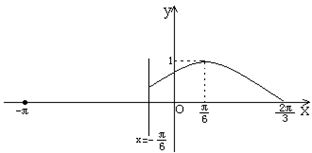 (1)求函数y=f(x)在[-p,
(1)求函数y=f(x)在[-p,![]() ]的表达式;
]的表达式;
(2)求方程f(x)=![]() 的解。
的解。