摘要:一元一次函数:.当时.是 函数,当时.是 函数,
网址:http://m.1010jiajiao.com/timu_id_4462818[举报]
| |||||||||||||||
已知关于x的函数y=f(x)=a
+b
+cx+d,x∈R(a,b,c,d为常数且a≠0),f'(x)=0是关于x的一元二次方程,根的判别式为△,给出下列四个结论:
①△<0是y=f(x)在(-∞,+∞)为单调函数的充要条件;
②若x1、x2分别为y=f(x)的极小值点和极大值点,则x2>x1;
③当a>0,△=0时,f(x)在(-∞,+∞)上单调递增;
④当c=3,b=0,a∈(0,1)时,y=f(x)在[-1,1]上单调递减.
其中正确结论的序号是 .(填写你认为正确的所有结论序号)
查看习题详情和答案>>
| x | 3 |
| x | 2 |
①△<0是y=f(x)在(-∞,+∞)为单调函数的充要条件;
②若x1、x2分别为y=f(x)的极小值点和极大值点,则x2>x1;
③当a>0,△=0时,f(x)在(-∞,+∞)上单调递增;
④当c=3,b=0,a∈(0,1)时,y=f(x)在[-1,1]上单调递减.
其中正确结论的序号是
已知关于x的函数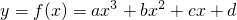 ,x∈R(a,b,c,d为常数且a≠0),f'(x)=0是关于x的一元二次方程,根的判别式为△,给出下列四个结论:
,x∈R(a,b,c,d为常数且a≠0),f'(x)=0是关于x的一元二次方程,根的判别式为△,给出下列四个结论:
①△<0是y=f(x)在(-∞,+∞)为单调函数的充要条件;
②若x1、x2分别为y=f(x)的极小值点和极大值点,则x2>x1;
③当a>0,△=0时,f(x)在(-∞,+∞)上单调递增;
④当c=3,b=0,a∈(0,1)时,y=f(x)在[-1,1]上单调递减.
其中正确结论的序号是________.(填写你认为正确的所有结论序号)
查看习题详情和答案>>
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案相应获得第二次优惠:
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为600元的商品,则消费金额为480元,480∈[400,500),所以获得第二次优惠金额为60元,获得的优惠总额为:600×0.2+60=180(元).
设购买商品的优惠率=
.
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
的优惠率?(取值范围用区间表示)
查看习题详情和答案>>
| 消费金额(元)的范围 | [200,400) | [400,500) | [500,700) | [700,900) | … |
| 第二次优惠金额(元) | 30 | 60 | 100 | 150 | … |
设购买商品的优惠率=
| 购买商品获得的优惠总额 |
| 商品的标价 |
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
| 1 |
| 3 |
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案相应获得第二次优惠:
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如:购买标价为600元的商品,则消费金额为480元,480∈[400,500),所以获得第二次优惠金额为60元,获得的优惠总额为:600×0.2+60=180(元).
设购买商品的优惠率=
.
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
的优惠率?(取值范围用区间表示)
查看习题详情和答案>>
| 消费金额(元)的范围 | [200,400) | [400,500) | [500,700) | [700,900) | … |
| 第二次优惠金额(元) | 30 | 60 | 100 | 150 | … |
设购买商品的优惠率=
| 购买商品获得的优惠总额 |
| 商品的标价 |
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
| 1 |
| 3 |