摘要：15．在数列{an}中.a1＝.并且对于任意n∈N*.且n>1时.都有an·an-1＝an-1-an成立.令bn＝(n∈N*)． (1)求数列{bn}的通项公式, 求数列{}的前n项和Tn.并证明Tn<-. (文)求数列{}的前n项和Tn. 解:(1)当n＝1时.b1＝＝3. 当n≥2时.bn-bn-1＝-＝＝1. ∴数列{bn}是首项为3.公差为1的等差数列. ∴数列{bn}的通项公式为bn＝n+2. . ∴Tn＝+++-++ ＝[]＝[-(+)] ＝[-]. ∵>＝. ∴-<-. ∴Tn<-. . ∴Tn＝+++-++ ＝[] ＝[-(+)] ＝.
网址：http://m.1010jiajiao.com/timu_id_4462658[举报]
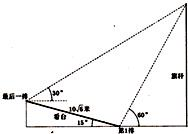北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，看台上第一排和最后一排的距离10| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10| 6 |
30
30
米．下表是最近十届奥运会的年份、届别、主办国，以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据：
某体育爱好组织，利用上表研究所获金牌数与主办奥运会之间的关系，
求出主办国在上届所获金牌数（设为x）与在当届所获金牌数（设为y）之间的线性回归方程
=
x+
，其中
=1.4，
在2008年第29届北京奥运会上英国获得19块金牌，则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为（所有金牌数精确到整数）
查看习题详情和答案>>
| 年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
| 届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 主办国家 | 联邦德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大利亚 | 希腊 | 中国 |
| 上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
| 当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
求出主办国在上届所获金牌数（设为x）与在当届所获金牌数（设为y）之间的线性回归方程
 |
| y |
|
| b |
|
| a |
|
| b |
在2008年第29届北京奥运会上英国获得19块金牌，则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为（所有金牌数精确到整数）
6、在2008年第29届北京奥运会上，我国代表团的金牌数雄踞榜首．如图是位居金牌榜前十二位的代表团获得的金牌数的茎叶图，则这十二个代表团获得的金牌数的平均数与中位数的差m的值为（ ）