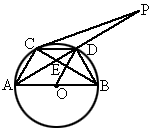
摘要:4.如图.AB是圆O的直径.P为圆外一点.PB是圆O的切线. PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与 PB交于D点.求证: (1)OD∥AP, (2)PD·PB=PC·OD. 证明:(1)连结OC.BC. 在△OCD和△OBD中 ∠OCD=∠OBD=90°. OB=OC.OD=OD. ∴△OCD≌△OBD. ∴∠BOD=∠COD=∠BOC. ① 又∠BOC与∠BAC分别是所对的圆心角和圆周角 ∴∠BOC=∠BAC. ② 由①②得∠BOD=∠BAC. ∴OD∥AP. (2)∵PB2=PC·PA. ③ 由(1)知OD∥AP.O为AB中点. ∴DO是△BPA的中位线. ∴PA=2OD.PB=2PD.代入③得 2PD·PB=PC·2OD. 即PD·PB=PC·OD.
网址:http://m.1010jiajiao.com/timu_id_4461698[举报]
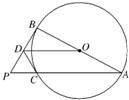 如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:
如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:(1)OD∥AP;
(2)PD•PB=PC•OD. 查看习题详情和答案>>
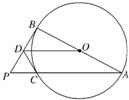 如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:
如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:
(1)OD∥AP;
(2)PD•PB=PC•OD.
查看习题详情和答案>>
如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:
(1)OD∥AP;
(2)PD•PB=PC•OD.
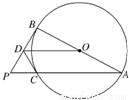 查看习题详情和答案>>
查看习题详情和答案>>
(1)OD∥AP;
(2)PD•PB=PC•OD.
 查看习题详情和答案>>
查看习题详情和答案>>
 的中点,连结AD并延长与过C点的切线交于P,OD与BC相交于E.
的中点,连结AD并延长与过C点的切线交于P,OD与BC相交于E.
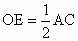 ;
;
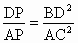 ;
;
 .求点A到平面PBC的距离.
.求点A到平面PBC的距离.