题目内容
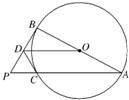 如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:
如图,AB是圆O的直径,P为圆外一点,PB是圆O的切线,PA是圆O的割线且与圆O相交于点C.过点C作圆O的切线与PB交于D点.求证:(1)OD∥AP;
(2)PD•PB=PC•OD.
分析:(1)连接OC及BC,因为PB和DC为圆O的切线,所以角OBD和角OCD相等且都为直角,则三角形OBD和三角形OCD都为直角三角形,由一对半径相等和一对公共边,利用“HL”的方法即可得到两直角三角形全等,根据全等三角形的对应角相等得到角BOD等于角COD都等于角BOC的一半,又根据同弧所对的圆心角等于所对弧的圆周角的2倍,得到角OAC也为角BOC的一半,进而得到角BOD等于角OAC,根据同位角相等,两直线平行,即可得证;
(2)根据切割线定理得到PB的平方等于PC与PA的积,由(1)得出的OD与PA平行和O为AB的中点,得到D也为BP的中点(得到PB等于2PD),进而得到OD为三角形BPA的中位线,根据中位线定理,得到PA等于2OD,然后把切割线定理得到关系式中的PB和PA等量代换,约分化简后即可得证.
(2)根据切割线定理得到PB的平方等于PC与PA的积,由(1)得出的OD与PA平行和O为AB的中点,得到D也为BP的中点(得到PB等于2PD),进而得到OD为三角形BPA的中位线,根据中位线定理,得到PA等于2OD,然后把切割线定理得到关系式中的PB和PA等量代换,约分化简后即可得证.
解答:证明:(1)连接OC,BC,
在△OCD和△OBD中
∠OCD=∠OBD=90°,
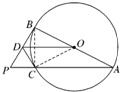
OB=OC,OD=OD,
∴直角△OCD≌直角△OBD,
∴∠BOD=∠COD=
∠BOC.①
又∠BOC与∠BAC分别是
所对的圆心角和圆周角
∴
∠BOC=∠BAC,②
由①②得∠BOD=∠BAC,
∴OD∥AP.
(2)∵PB2=PC•PA,③
由(1)知OD∥AP,O为AB中点,
∴DO是△BPA的中位线,
∴PA=2OD,PB=2PD,代入③得
2PD•PB=PC•2OD,
即PD•PB=PC•OD.
在△OCD和△OBD中
∠OCD=∠OBD=90°,

OB=OC,OD=OD,
∴直角△OCD≌直角△OBD,
∴∠BOD=∠COD=
| 1 |
| 2 |
又∠BOC与∠BAC分别是
 |
| BC |
∴
| 1 |
| 2 |
由①②得∠BOD=∠BAC,
∴OD∥AP.
(2)∵PB2=PC•PA,③
由(1)知OD∥AP,O为AB中点,
∴DO是△BPA的中位线,
∴PA=2OD,PB=2PD,代入③得
2PD•PB=PC•2OD,
即PD•PB=PC•OD.
点评:此题考查学生灵活运用“HL”的方法证明两直角三角形全等,掌握切线的性质及切割线定理,要求学生善于观察图形寻找角与角之间存在的关系,培养学生的逻辑思维能力,是一道中档题.

练习册系列答案
相关题目


 如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.
如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.



 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数