摘要：(二)研探新知 1．我们已经知道.函数是建立在两个非空数集间的一种对应.若将其中的条件“非空数集 弱化为“任意两个非空集合 .按照某种法则可以建立起更为普通的元素之间的对应关系.这种对应就叫映射． 2．先看几个例子.两个集合A.B的元素之间的一些对应关系: (1)开平方, (2)求正弦, (3)求平方, (4)乘以2． 归纳引出映射概念: 一般地.设A.B是两个非空的集合.如果按某一个确定的对应法则.使对于集合A中的任意一个元素.在集合B中都有唯一确定的元素与之对应.那么就称对应:A→B为从集合A到集合B的一个映射． 记作“:A→B 说明: (1)这两个集合有先后顺序.A到B的映射与B到A的映射是截然不同的.其中表示具体的对应法则.可以用多种形式表述． (2)“都有唯一 什么意思? 包含两层意思:一是必有一个,二是只有一个.也就是说有且只有一个的意思．
网址：http://m.1010jiajiao.com/timu_id_4460142[举报]
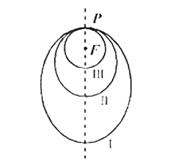
如图所示，2010年10月1日“嫦娥二号”探月卫星沿地月转移轨道飞向月球，在月球附近一点
变轨进入以月球球心
为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在点第二次变轨进入仍以为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在点第三次变轨进入以为圆心的圆形轨道Ⅲ绕月飞行，若用
和
分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用
和
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：
①
； ②
；
③
； ④
＜
.
其中正确式子的序号是 ▲ .
查看习题详情和答案>>如图所示，2010年10月1日“嫦娥二号”探月卫星沿地月转移轨道飞向月球，在月球附近一点
变轨进入以月球球心
为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在点第二次变轨进入仍以为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在点第三次变轨进入以为圆心的圆形轨道Ⅲ绕月飞行，若用
和
分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用
和
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：
①
； ②
；
③
； ④
＜
.
其中正确式子的序号是 ▲ .
查看习题详情和答案>>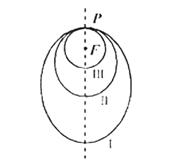
变轨进入以月球球心
为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在
和
分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用
和
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：
①
； ②
； 
； ④
＜
.