摘要：(五)归纳小结 ①从具体实例引入了函数的概念.用集合与对应的语言描述了函数的定义及其相关概念,②初步介绍了求函数定义域和判断同一函数的基本方法.同时引出了区间的概念.
网址：http://m.1010jiajiao.com/timu_id_4460121[举报]
以下五个命题
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②样本方差反映了样本数据与样本平均值的偏离程度；
③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
④在回归直线方程
=0.1x+10中，当解释变量x每增加一个单位时，预报变量
增加0.1个单位；
⑤在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．
其中正确的是（ ）
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②样本方差反映了样本数据与样本平均值的偏离程度；
③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
④在回归直线方程
| ? |
| y |
| ? |
| y |
⑤在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．
其中正确的是（ ）
| A、②③④⑤ | B、①③④ |
| C、①③⑤ | D、②④ |
某商场共五层，从五层下到四层有3个出口，从三层下到二层有4个出口，从二层下到一层有4个出口，从一层走出商场有6个出口．安全部门在每层安排了一名警员值班，负责该层的安保工作．假设每名警员到该层各出口处的时间相等，某罪犯在五楼犯案后，欲逃出商场，各警员同时接到指令，选择一个出口进行围堵．逃犯在每层选择出口是等可能的．已知他被三楼警员抓获的概率为
．
（Ⅰ）问四层下到三层有几个出口？
（Ⅱ）天网恢恢，疏而不漏，犯罪嫌疑人最终落入法网．设抓到逃犯时，他已下了ξ层楼，写出ξ的分布列，并求Eξ．
查看习题详情和答案>>
| 1 | 9 |
（Ⅰ）问四层下到三层有几个出口？
（Ⅱ）天网恢恢，疏而不漏，犯罪嫌疑人最终落入法网．设抓到逃犯时，他已下了ξ层楼，写出ξ的分布列，并求Eξ．
读算法，完成该题：第一步，李同学拿出一正方体；第二步，把正方体表面全涂上红色；第三步，将该正方体切割成27个全等的小正方体；第四步，将这些小正方体放到一箱子里，搅拌均匀；第五步，从箱子里随机取一个小正方体．问：取到的小正方体恰有三个面为红色的概率是（ ）
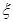表示获奖人数，求
。
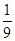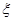层楼，写出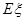
。