摘要:22.已知对于任意的实数x.不等式|x+1|-|x-2|>k恒成立.求出实数k的取值范围. [解答一]∵ ∴.欲不等式|x+1|-|x-2|>k恒成立.当且仅当k小于的最小值时.∴k的取值范围是(). [解答二]要使不等式|x+1|-|x-2|>k恒成立.只要代数式|x+1|-|x-2|的最小值大于k.反之即要求k小于代数式|x+1|-|x-2|的最小值, 注意到|x+1|的几何意义为数轴上的点x到-1的距离.|x-2|的几何意义为点x到2的距离.由于这两个距离之差的最小值显然是-3.∴只需k<-3.故k的取值范围是().
网址:http://m.1010jiajiao.com/timu_id_4460016[举报]
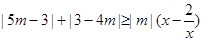 恒成立,则
恒成立,则