摘要：20．已知椭圆E:(a>b>0),以F1(-c,0)为圆心.以a-c为半径作圆F1.过点B2(0,b)作圆F1的两条切线.设切点为M.N. (1)若过两个切点M.N的直线恰好经过点B1(0,-b)时.求此椭圆的离心率; (2)若直线MN的斜率为-1,且原点到直线MN的距离为4(-1),求此时的椭圆方程, (3)是否存在椭圆E.使得直线MN的斜率k在区间(-)内取值?若存在.求出椭圆E的离心率e的取值范围,若不存在.请说明理由.

网址：http://m.1010jiajiao.com/timu_id_4458370[举报]

（2012•佛山二模）已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个交点为F1(-
3
，0)，而且过点H(
3
，
1
2
)．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设椭圆E的上下顶点分别为A1，A2，P是椭圆上异于A1，A2的任一点，直线PA1，PA2分别交x轴于点N，M，若直线OT与过点M，N的圆G相切，切点为T．证明：线段OT的长为定值，并求出该定值．
 查看习题详情和答案>>
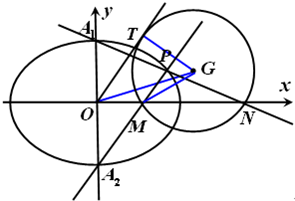（2012•佛山二模）已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点为F1（-
3
，0），而且过点H（
3
，
1
2
）．
（1）求椭圆E的方程；
（2）设椭圆E的上下顶点分别为A1，A2，P是椭圆上异于A1，A2的任一点，直线OT与过点M，N的圆G相切，切点为G．证明：线段OT的长为定值．
 查看习题详情和答案>>
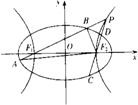如图，已知椭圆E：
x2
8
+
y2
4
=1焦点为F1、F2，双曲线G：x2-y2=4，设P是双曲线G上异于顶点的任一点，直线PF1、PF2与椭圆的交点分别为A、B和C、D．
（1）设直线PF1、PF2的斜率分别为k1和k2，求k1•k2的值；
（2）是否存在常数λ，使得|AB|+|CD|=λ|AB|•|CD|恒成立？若存在，试求出λ的值；若不存在，请说明理由．
 查看习题详情和答案>>
如图，已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0），焦点为F1、F2，双曲线G：x2-y2=m（m＞0）的顶点是该椭圆的焦点，设P是双曲线G上异于顶点的任一点，直线PF1、PF2与椭圆的交点分别为A、B和C、D，已知三角形ABF2的周长等于8
2
，椭圆四个顶点组成的菱形的面积为8
2
．
（1）求椭圆E与双曲线G的方程；
（2）设直线PF1、PF2的斜率分别为k1和k2，探求k1和k2的关系；
（3）是否存在常数λ，使得|AB|+|CD|=λ|AB|•|CD|恒成立？若存在，试求出λ的值；若不存在，请说明理由．
精英家教网 查看习题详情和答案>>
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率e=
2
2
，点D（0，1）在且椭圆E上，
（Ⅰ）求椭圆E的方程；
（Ⅱ）设过点F2且不与坐标轴垂直的直线交椭圆E于A、B两点，线段AB的垂直平分线与x轴交于点G（t，0），求点G横坐标的取值范围．
（Ⅲ）试用表示△GAB的面积，并求△GAB面积的最大值．
 查看习题详情和答案>>

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网