摘要:18.下列有关操作及实验现象的描述正确的是 A.铁丝在氧气中燃烧生成四氧化三铁 B.用湿润的蓝色石蕊试纸检验氨气时.试纸变为红色 C.向蛋清溶液中滴几滴浓硝酸.微热.出现黄色 △ D.含碘酸钾(KIO3)的食盐水滴在馒头片上.出现蓝色 19.铜与浓硫酸共热的条件下可以发生化学反应Cu + 2H2SO4===CuSO4 + SO2↑ + 2H2O.但 是在工业上制取硫酸铜不是直接利用浓硫酸与铜反应.而是将铜屑在空气中加热氧化.然 后浸入稀硫酸中反应过滤.并反复加热和浸入操作.你认为这样的优点是 A.节约能源 B.不产生污染大气的二氧化硫 C.提高硫酸的利用率 D.提高铜的利用率
网址:http://m.1010jiajiao.com/timu_id_4457529[举报]
红细胞含有大量的血红蛋白,红细胞的机能主要是由血红蛋白完成,血红蛋白的主要功能是携带氧气或二氧化碳,我们可以选用猪、牛、羊或其他脊椎动物的血液进行实验,来提取和分离血红蛋白,请回答下列有关问题:
(1)血红蛋白提取和分离的程度可分为四步:样品处理、___________、___________
和纯度鉴定。
(2)实验前取新鲜的血液,要切记在采血容器中预先加入柠檬酸钠,取血回来,马上
进行离心,收集血红蛋白溶液。
①加入柠檬酸钠的目的是______________________________。
②以上所述的过程即是样品处理,它包括____________________、血红蛋白的释放、离心等操作收集血红蛋白溶液。
(3)收集的血红蛋白溶液在透析袋中可以经过透析,这就是样品的粗分离。
①透析的目的是__________________________________________________。
②透析的原理是_______________________________________ _________
_____________________________________________________________________。 查看习题详情和答案>>
(1)血红蛋白提取和分离的程度可分为四步:样品处理、___________、___________
和纯度鉴定。
(2)实验前取新鲜的血液,要切记在采血容器中预先加入柠檬酸钠,取血回来,马上
进行离心,收集血红蛋白溶液。
①加入柠檬酸钠的目的是______________________________。
②以上所述的过程即是样品处理,它包括____________________、血红蛋白的释放、离心等操作收集血红蛋白溶液。
(3)收集的血红蛋白溶液在透析袋中可以经过透析,这就是样品的粗分离。
①透析的目的是__________________________________________________。
②透析的原理是_______________________________________ _________
_____________________________________________________________________。 查看习题详情和答案>>
 如图,已知在8×8的网格中,每个小正方形的边长都是1,请按下列要求操作或解答:
如图,已知在8×8的网格中,每个小正方形的边长都是1,请按下列要求操作或解答:(1)将图中的格点三角形ABC平移,使点A平移至点A′,画出平移后的△A′B′C′,并求出△A′B′C′的面积;
(2)利用网格找出格点(点A除外),使得以该点及点B、点C为顶点的三角形与三角形ABC面积相等,请画出所满足条件的格点(用字母A1、A2等表示)
(2012•内江)某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
查看习题详情和答案>>
| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
23、如图,四边形ABCD是正方形,CE是∠BCD的外角∠DCF的平分线.
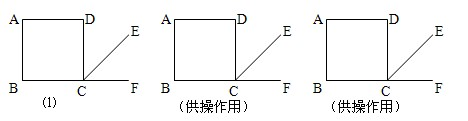
(如果需要,还可以继续操作、实验与测量)
(1)操作实验:将直角尺的直角顶点P在边BC上移动(与点B、C不重合),且一直角边经过点A,另一直角边与射线CE交于点Q,不断移动P点,同时测量线段PQ与线段PA的长度,完成下列表格(精确到0.1cm).

(2)观测测量结果,猜测它们之间的关系:
(3)对你猜测的结论是否成立均进行说明理由;
(4)当点P在BC的延长线上移动时,继续(1)的操作实验,试问:(1)中的猜测结论还成立吗?若成立,请给出理由;若不成立,也请说明理由.
查看习题详情和答案>>

(如果需要,还可以继续操作、实验与测量)
(1)操作实验:将直角尺的直角顶点P在边BC上移动(与点B、C不重合),且一直角边经过点A,另一直角边与射线CE交于点Q,不断移动P点,同时测量线段PQ与线段PA的长度,完成下列表格(精确到0.1cm).

(2)观测测量结果,猜测它们之间的关系:
PA=PQ
;(3)对你猜测的结论是否成立均进行说明理由;
(4)当点P在BC的延长线上移动时,继续(1)的操作实验,试问:(1)中的猜测结论还成立吗?若成立,请给出理由;若不成立,也请说明理由.
两个重叠的正多边形,其中的一个绕某一个顶点旋转所形成的有关问题.
实验与论证
设旋转角∠A1AOB1=α(α<∠A1AOA2),θ3,θ4,θ5,θ6所表示的角如图所示.
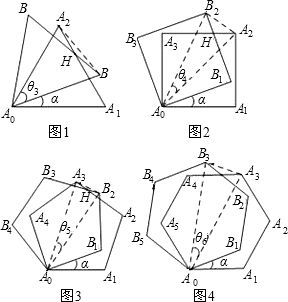
(1)用含α的式子表示角的度数:θ3= ,θ4= ,θ5= ;
(2)图2中,连接AoH时,在不添加其他辅助线的情况下,是否存在与直线AoH垂直且被它平分的线段?若存在,请给出证明;若不存在,请说明理由;
归纳与猜想
设正n边形AOA1A2…An-1与正n边形AOB1B2…Bn-1重合(其中A1与B1重合),现将正n边形AOB1B2…Bn-1绕顶点Ao逆时针旋转α(0°<α<
).
(3)试猜想在正n边形的情况下,是否存在以A1为端点的线段被直线AoH垂直且平分?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.
(4)设θn与上述“θ3,θ4,…”的意义一样,请直接写出θn的度数. 查看习题详情和答案>>
实验与论证
设旋转角∠A1AOB1=α(α<∠A1AOA2),θ3,θ4,θ5,θ6所表示的角如图所示.

(1)用含α的式子表示角的度数:θ3=
(2)图2中,连接AoH时,在不添加其他辅助线的情况下,是否存在与直线AoH垂直且被它平分的线段?若存在,请给出证明;若不存在,请说明理由;
归纳与猜想
设正n边形AOA1A2…An-1与正n边形AOB1B2…Bn-1重合(其中A1与B1重合),现将正n边形AOB1B2…Bn-1绕顶点Ao逆时针旋转α(0°<α<
| 180° | n |
(3)试猜想在正n边形的情况下,是否存在以A1为端点的线段被直线AoH垂直且平分?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.
(4)设θn与上述“θ3,θ4,…”的意义一样,请直接写出θn的度数. 查看习题详情和答案>>