摘要：22．如图12.直线交x轴于点A.交y轴于点B.抛物线的顶点为A.且经过点B． ⑴求该抛物线的解析式, ⑵若点C(m.)在抛物线上.求m的值．
网址：http://m.1010jiajiao.com/timu_id_4455657[举报]
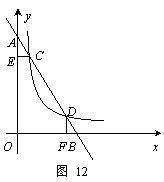
如图12，在平面直角坐标系中，直线AB与y轴、x轴分别交于点A、点B，与双曲线
交于点C（1，6）、D（3，n）两点，
轴于点E，
轴于点F.
（1）填空：
，
；
（2）求直线AB的解析式；
（3）求证：
.
如图12-1，已知直线y= -x+4交x轴于点A，交y轴于点B．
（1）写出A、B两点的坐标分别是： ；
（2）设点P是射线y = x（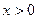
）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）
查看习题详情和答案>>
（1）写出A、B两点的坐标分别是： ；
（2）设点P是射线y = x（
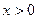）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）
查看习题详情和答案>>
如图12-1，已知直线y= -x+4交x轴于点A，交y轴于点B．
（1）写出A、B两点的坐标分别是： ；
（2）设点P是射线y = x（
）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）
（1）写出A、B两点的坐标分别是： ；
（2）设点P是射线y = x（
）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）
）上一点，点P的横坐标为t，M是OP的中点（O是原点），以PM为对角线作正方形PDME．正方形PDME与△OAB公共部分的面积为S，求S与t之间的函数关系式，并求S的最大值．（图12-2、12-3供你探索问题时使用）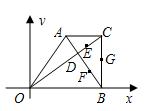
27、如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB=18，BC=12，AC=9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点，以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图象上的是（ ）