摘要： X.Y.Z.L.M五种元素的原子序数依次增大.X.Y.Z.L是组成蛋白质的基础元素.M是地壳中含量最高的金属元素. 回答下列问题: ⑴ L的元素符号为 ,M在元素周期表中的位置为 ,五种元素的原子半径从大到小的顺序是 . ⑵ Z.X两元素按原子数目比l∶3和2∶4构成分子A和B.A的电子式为 .B的结构式为 . ⑶ 硒(se)是人体必需的微量元素.与L同一主族.Se原子比L原子多两个电子层.则Se的原子序数为 .其最高价氧化物对应的水化物化学式为 .该族2 ~ 5周期元素单质分别与H2反应生成l mol气态氢化物的反应热如下.表示生成1 mol硒化氢反应热的是 . a．+99.7 mol·L-1 b．+29.7 mol·L-1 c．-20.6 mol·L-1 d．-241.8 kJ·mol-1 ⑷ 用M单质作阳极.石墨作阴极. NaHCO3溶液作电解液进行电解.生成难溶物R.R受热分解生成化合物Q .写出阳极生成R的电极反应式: ,由R生成Q的化学方程式: .
网址：http://m.1010jiajiao.com/timu_id_4454075[举报]
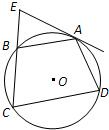
附加题：A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
求证：AB2=BE•CD．
B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足
|
|
C．已知椭圆C的极坐标方程为ρ2=
| 12 |
| 3cos2θ+4sin2θ |
|
D．已知x，y，z均为正数．求证：
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
若直线l与x、y轴分别交于A（a，0），B（0，b），ab≠0，则直线l的截距式方程为
+
=1，若平面α与x、y、z轴分别交于A（a，0，0），B（0，b，0），C（0，0，c），abc≠0，则平面α的截距式方程为
+
+
=1；由点P（x0，y0）到直线Ax+By+C=0的距离d=
类比到空间有：点M（x0，y0，z0）到平面Ax+By+Cz+D=0的距离d=
．
查看习题详情和答案>>
| x |
| a |
| y |
| b |
| x |
| a |
| y |
| b |
| z |
| c |
| |Ax0+By0+C| | ||
|
| |Ax0+By0+Cz0+D| | ||
|
| |Ax0+By0+Cz0+D| | ||
|
本题有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分
（1）二阶矩阵M对应的变换将向量
，
分别变换成向量
，
，直线l在M的变换下所得到的直线l′的方程是2x-y-1=0，求直线l的方程．
（2）过点P（-3，0）且倾斜角为30°的直线l和曲线C：
（s为参数）相交于A，B两点，求线段AB的长．
（3）若不等式|a-1|≥x+2y+2z，对满足x2+y2+z2=1的一切实数x，y，z恒成立，求实数a的取值范围． 查看习题详情和答案>>
（1）二阶矩阵M对应的变换将向量
|
|
|
|
（2）过点P（-3，0）且倾斜角为30°的直线l和曲线C：
|
（3）若不等式|a-1|≥x+2y+2z，对满足x2+y2+z2=1的一切实数x，y，z恒成立，求实数a的取值范围． 查看习题详情和答案>>
选修4-2：矩阵及其变换（1）如图，向量
| OA |
| OB |
| OA′ |
| OB′ |
（Ⅰ）求矩阵M；
（Ⅱ）并求y=sin(x+
| π |
| 3 |
选修4-4：坐标系与参数方程
（ 2）在直角坐标系x0y中，直线l的参数方程为
|
| 5 |
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线l交于点A，B．若点P的坐标为（3，
| 5 |
选修4-5：不等式选讲
（3）已知x，y，z为正实数，且
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．A．选修4-1：（几何证明选讲）
如图，从O外一点P作圆O的两条切线，切点分别为A，B，
AB与OP交于点M，设CD为过点M且不过圆心O的一条弦，
求证：O，C，P，D四点共圆．
B．选修4-2：（矩阵与变换）
已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
1 1 |
C．选修4-4：（坐标系与参数方程）
在极坐标系中，曲线C的极坐标方程为p=2
| 2 |
| π |
| 4 |
|
D．选修4-5（不等式选讲）
已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．