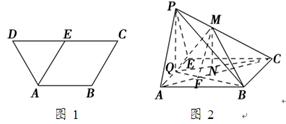
摘要:6.如图.在等腰梯形中.AB∥CD.AD=12 cm.AC交梯形 中位线EG于点F.若EF=4 cm.FG=10 cm.求此梯形的 面积. 解:如图所示.作高DM.CN.则四边形DMNC为矩形. ∵EG是梯形ABCD的中位线. ∴EG∥DC∥AB. ∴F是AC的中点. ∴DC=2EF=8.AB=2FG=20.MN=DC=8. 在Rt△ADM和Rt△BCN中. AD=BC.∠DAM=∠CBN.∠AMD=∠BNC=90°. ∴△ADM≌△BCN. ∴AM=BN==6. ∴DM===6. ∴S梯形=EG·DM=14×6=84 (cm2).
网址:http://m.1010jiajiao.com/timu_id_4453887[举报]
如图①,在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图②,将△ABE沿AE折起,使二面角BAEC成直二面角,连结BC、BD,F是CD的中点,P是棱BC的中点.求证:
图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.
如图①,在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图②,将△ABE沿AE折起,使二面角BAEC成直二面角,连结BC、BD,F是CD的中点,P是棱BC的中点.求证:
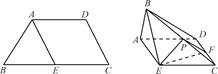
图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.

图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.
如图①,在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图②,将△ABE沿AE折起,使二面角BAEC成直二面角,连结BC、BD,F是CD的中点,P是棱BC的中点.求证:
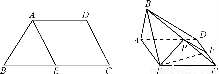
图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.
查看习题详情和答案>>