摘要:如图11-8所示的电路.已知电池电动势E=90 V.内阻r=5 Ω.R1=10 Ω.R2=20 Ω.板面水平放置的平行板电容器的两极板M.N相距d=3 cm.在两板间的正中央有一带电液滴.其电量q=-2×10-7 C.其质量m=4.5×10-5 kg.取g=10 m/s2.问 (1)若液滴恰好能静止平衡时.滑动变阻器R的滑动头C正好在正中点.那么滑动变阻器的最大阻值Rm是多大? (2)将滑动片C迅速滑到A端后.液滴将向哪个极板做什么运动?到达极板时的速度是多大?
网址:http://m.1010jiajiao.com/timu_id_4453279[举报]
两条光滑的水平金属导轨彼此平行,置于桌边,金属棒ab架在两导轨端点上并与导轨垂直,导轨区域内有竖直向下的匀强磁场,导轨另一端与电池、电容器连成电路,如图15-2-11所示.已知金属棒的质量m=5×10-3kg,两导轨间距L=1.0 m,电池电动势E=16 V,电容器的电容量C=200 μF,磁场的磁感应强度B=0.5 T,金属棒在通电后受安培力作用而平抛出去,下落高度h=0.8 m,抛出落地水平位移S=0.064 m.试求开关K先接1,再接2,金属棒被抛出后电容器上电压的数值.
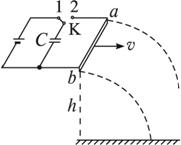
图15-2-11
查看习题详情和答案>>两条光滑的水平金属导轨彼此平行,置于桌边,金属棒ab架在两导轨端点上并与导轨垂直,导轨区域内有竖直向下的匀强磁场,导轨另一端与电池、电容器连成电路,如图15-2-11所示.已知金属棒的质量m=5×10-3kg,两导轨间距L=1.0 m,电池电动势E=16 V,电容器的电容量C=200 μF,磁场的磁感应强度B=0.5 T,金属棒在通电后受安培力作用而平抛出去,下落高度h=0.8 m,抛出落地水平位移S=0.064 m.试求开关K先接1,再接2,金属棒被抛出后电容器上电压的数值.
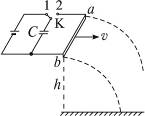
图15-2-11
查看习题详情和答案>>两条光滑的水平金属导轨彼此平行,置于桌边,金属棒ab架在两导轨端点上并与导轨垂直,导轨区域内有竖直向下的匀强磁场,导轨另一端与电池、电容器连成电路,如图15-2-11所示.已知金属棒的质量m=5×10-3kg,两导轨间距L="1.0" m,电池电动势E="16" V,电容器的电容量C="200" μF,磁场的磁感应强度B="0.5" T,金属棒在通电后受安培力作用而平抛出去,下落高度h="0.8" m,抛出落地水平位移S="0.064" m.试求开关K先接1,再接2,金属棒被抛出后电容器上电压的数值.

图15-2-11

图15-2-11
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图1所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.

①关于该实验,下列说法正确的是
A.打点计时器可以用直流电源供电,电压为4~6V
B.实验中使用的若干根橡皮筋的原长可以不相等
C.每次实验中应使小车从同一位置由静止弹出
D.利用每次测出的小车最大速度vm和橡皮筋做的功W,依次做出W-vm、W-vm2、W-vm3、W2-vm、W3-vm…的图象,得出合力做功与物体速度变化的关系.
②图2给出了某次在正确操作情况下打出的纸带,从中截取了测量物体最大速度所用的一段纸带,测得O点到A、B、C、D、E各点的距离分别为OA=5.65cm,OB=7.12cm,OC=8.78cm,OD=10.40cm,OE=11.91cm,.已知相邻两点打点时间间隔为0.02s,则小车获得的最大速度vm=
(2)有一根细长而均匀的金属管线样品,长约为60cm,电阻大约为6Ω.横截面如图3所示.
①用螺旋测微器测量金属管线的外径,示数如图4所示,金属管线的外径为
②现有如下器材
A.电流表(量程0.6A,内阻约0.1Ω)
B.电流表(量程3A,内阻约0.03Ω)
C.电压表(量程3V,内阻约3kΩ)
D.滑动变阻器(1750Ω,0.3A)
E.滑动变阻器(15Ω,3A)
F.蓄电池(6V,内阻很小)
G.开关一个,带夹子的导线若干
要进一步精确测量金属管线样品的阻值,电流表应选
③请将图5所示的实际测量电路补充完整.
④已知金属管线样品材料的电阻率为ρ,通过多次测量得出金属管线的电阻为R,金属管线的外径为d,要想求得金属管线内形状不规则的中空部分的截面积S,在前面实验的基础上,还需要测量的物理量是
-
-
.
查看习题详情和答案>>

①关于该实验,下列说法正确的是
CD
CD
.A.打点计时器可以用直流电源供电,电压为4~6V
B.实验中使用的若干根橡皮筋的原长可以不相等
C.每次实验中应使小车从同一位置由静止弹出
D.利用每次测出的小车最大速度vm和橡皮筋做的功W,依次做出W-vm、W-vm2、W-vm3、W2-vm、W3-vm…的图象,得出合力做功与物体速度变化的关系.
②图2给出了某次在正确操作情况下打出的纸带,从中截取了测量物体最大速度所用的一段纸带,测得O点到A、B、C、D、E各点的距离分别为OA=5.65cm,OB=7.12cm,OC=8.78cm,OD=10.40cm,OE=11.91cm,.已知相邻两点打点时间间隔为0.02s,则小车获得的最大速度vm=
0.82
0.82
m/s.(2)有一根细长而均匀的金属管线样品,长约为60cm,电阻大约为6Ω.横截面如图3所示.
①用螺旋测微器测量金属管线的外径,示数如图4所示,金属管线的外径为
1.125
1.125
mm;②现有如下器材
A.电流表(量程0.6A,内阻约0.1Ω)
B.电流表(量程3A,内阻约0.03Ω)
C.电压表(量程3V,内阻约3kΩ)
D.滑动变阻器(1750Ω,0.3A)
E.滑动变阻器(15Ω,3A)
F.蓄电池(6V,内阻很小)
G.开关一个,带夹子的导线若干
要进一步精确测量金属管线样品的阻值,电流表应选
A
A
,滑动变阻器应选E
E
.(只填代号字母).③请将图5所示的实际测量电路补充完整.
④已知金属管线样品材料的电阻率为ρ,通过多次测量得出金属管线的电阻为R,金属管线的外径为d,要想求得金属管线内形状不规则的中空部分的截面积S,在前面实验的基础上,还需要测量的物理量是
管线长度L
管线长度L
.计算中空部分截面积的表达式为S=| πd2 |
| 4 |
| ρL |
| R |
| πd2 |
| 4 |
| ρL |
| R |
影响物质材料电阻率的因素很多.一般金属材料的电阻率随温度的升高而增大;半导体材料的电阻率则随温度的升高而减小;
(1)如图(甲)是由某金属材料制成的电阻R随摄氏温度t变化的图象,若用该电阻与电池(电动势E=1.5V,内阻不计)、电流表(量程为5mA、内阻Rg=100Ω)、电阻箱R′串联起来,连接成如图(乙)所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,就得到了一个简单的“金属电阻温度计”.
①电流刻度较大处对应的温度刻度值 ;(填“较大”或“较小”)
②若电阻箱阻值R′=50Ω,在丙图中空格处(5mA)对应的温度数值为 ℃.
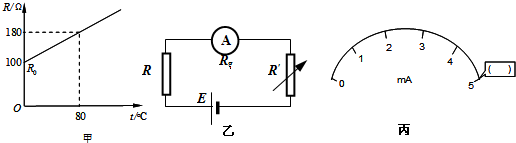
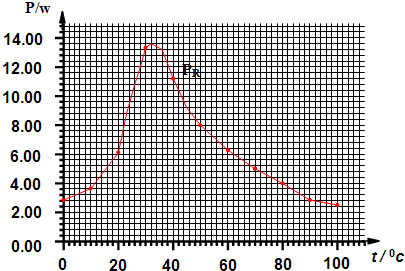
(2)PTC元件由于材料的原因有特殊的导电特性,其电阻随温度变化关系复杂.现有一只由PTC元件做成的加热器,实验测出各温度下它的阻值,数据如下:
加热器接到200V的电源上,在方格纸上已根据反复实验的大量实验数据作出了PTC加热器功率PR随温度t的变化关系曲线,已知PTC加热器器外表面向四周散热的功率为PQ=0.1(t-t0)瓦,其中t(单位为℃)为加热器的温度,t0为室温(本题取20℃).
①请在同一坐标平面内作出PQ与温度t之间关系的图象
②加热器工作的稳定温度为 ℃;
③加热器保持工作稳定温度的原理为:
当温度稍高于稳定温度时: ;
当温度稍低于稳定温度时: 从而保持温度稳定.
查看习题详情和答案>>
(1)如图(甲)是由某金属材料制成的电阻R随摄氏温度t变化的图象,若用该电阻与电池(电动势E=1.5V,内阻不计)、电流表(量程为5mA、内阻Rg=100Ω)、电阻箱R′串联起来,连接成如图(乙)所示的电路,用该电阻做测温探头,把电流表的电流刻度改为相应的温度刻度,就得到了一个简单的“金属电阻温度计”.
①电流刻度较大处对应的温度刻度值
②若电阻箱阻值R′=50Ω,在丙图中空格处(5mA)对应的温度数值为

(2)PTC元件由于材料的原因有特殊的导电特性,其电阻随温度变化关系复杂.现有一只由PTC元件做成的加热器,实验测出各温度下它的阻值,数据如下:
| t/℃ | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| R/kΩ | 14 | 11 | 7 | 3 | 4 | 5 | 6 | 8 | 10 | 14 | 16 |
①请在同一坐标平面内作出PQ与温度t之间关系的图象
②加热器工作的稳定温度为
③加热器保持工作稳定温度的原理为:
当温度稍高于稳定温度时:
当温度稍低于稳定温度时:
