摘要:例1.已知.且..求的值. 例2.计算: 例3.若且..求的值. 例4.已知.问是否存在满足的.使得的值不随的变化而变化?如果存在.求出的值,若不存在.说明理由. 例5.已知为第二象限的角..为第一象限的角..求的值. 例6.已知. (I)求sinx-cosx的值, (Ⅱ)求的值.
网址:http://m.1010jiajiao.com/timu_id_4452510[举报]
毛毛的计算器中的“开根号”键最近“感冒”了,输出的结果千奇百怪.细心的毛毛在复习资料上发现有一个真命题:已知对于任意正数a、b,![]() ≠
≠![]() ,则
,则![]() 一定在
一定在![]() 和
和![]() 之间;并且
之间;并且![]() 比
比![]() 更接近
更接近![]() .毛毛自己编制了一个算法来求
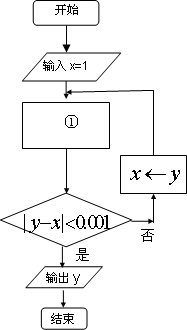
.毛毛自己编制了一个算法来求![]() 的近似值(如图).请你在①中填上适当赋值语句:y←________.
的近似值(如图).请你在①中填上适当赋值语句:y←________.
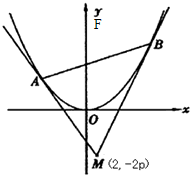 已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且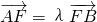 (λ>0),
(λ>0),
过A、B两点分别作抛物线的切线,设其交点为M.
(1)证明线段FM被x轴平分;
(2)计算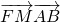 的值;
的值;
(3)求证: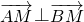 .
.
查看习题详情和答案>>
已知抛物线x2=8y的焦点为F,A、B是抛物线上的两动点,且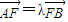 (λ>0),
(λ>0),
过A、B两点分别作抛物线的切线,设其交点为M.
(1)证明线段FM被x轴平分;
(2)计算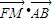 的值;
的值;
(3)求证: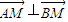 .
.
 查看习题详情和答案>>
查看习题详情和答案>>
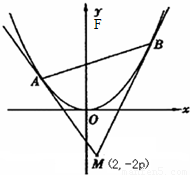
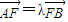 (λ>0),
(λ>0),过A、B两点分别作抛物线的切线,设其交点为M.
(1)证明线段FM被x轴平分;
(2)计算
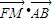 的值;
的值;(3)求证:
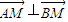 .
. 查看习题详情和答案>>
查看习题详情和答案>>
【选做题】在A,B,C,D四小题中只能选做2题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤.
21-1.(选修4-2:矩阵与变换)
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆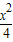 +
+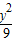 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.
21-2.(选修4-4:参数方程)
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为(4, ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 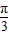 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.
(1)求直线l关于t的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
查看习题详情和答案>>
21-1.(选修4-2:矩阵与变换)
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆
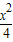 +
+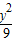 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.21-2.(选修4-4:参数方程)
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为(4,
 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 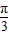 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.(1)求直线l关于t的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
查看习题详情和答案>>
【选做题】在A,B,C,D四小题中只能选做2题,每题10分,共计20分.请在答题卡指定区域内作答,解答时写出文字说明、证明过程或演算步骤.
21-1.(选修4-2:矩阵与变换)
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆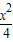 +
+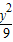 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.
21-2.(选修4-4:参数方程)
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为(4,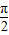 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 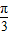 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.
(1)求直线l关于t的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
查看习题详情和答案>>
21-1.(选修4-2:矩阵与变换)
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆
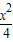 +
+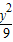 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.21-2.(选修4-4:参数方程)
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为(1,-5),点M的极坐标为(4,
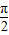 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 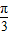 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.(1)求直线l关于t的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
查看习题详情和答案>>