摘要:21.解:设甲预报站预测准确为事件.乙预报站预测准确为事件. 1)甲.乙两个天气预报站同时预报准确的概率为: , 2)至少有一个预报站预报准确的概率= 3)如果甲站独立预报三次.其中恰有两次预报准确的概率为 22.1)证明:取的中点.连.. ∵⊥.⊥. ∴平面. 又∵.分别是.的中点. ∴∥ ∴⊥平面.∵平面 ∴⊥ .又∵.且为的中点.故由平面几 何知识可知.又∵∥.∴∥ ∴...共面. ∴⊥平面.∴⊥. 2)解:作于.∵平面.∴.∴平面.作于.连.由三垂线定理得.∴为二面角的一个平面角. 在中.= 又∵平面.∴ 又.∴⊥平面.∴ 易得=.=. ∴在中. =. 又在中.=.. 23 解:(1)当n=1时.左边=1+1=2=.右边=.不等式显然成立. (2)假设n=k时.不等式成立.即 ->.? 那么.当n=k+1时. [-]>=·. ?∵ (·3-()3=3/2)-3-22)=2)>0. ∴ ·>=. ? ∴ 当n=k+1时.不等式亦成立. 由证明知.不等式对一切n∈N都成立. 说明:在第二步证明·>时.我们还用到了比较法.
网址:http://m.1010jiajiao.com/timu_id_4450462[举报]
在同一时间段里,有甲乙两个天气预报站相互独立的对天气进行预测,根据以往的统计规律,甲预报站对天气预测的准确率为0.8,乙预报站对天气预测的准确率为0.75,求在同一时间段内
(Ⅰ)甲乙两个天气预报站同时预报准确的概率;
(Ⅱ)至少有一个预报站预报准确的概率;
(Ⅲ)如果甲站独立预报3次,其中恰有两次预报准确的概率 查看习题详情和答案>>
(Ⅰ)甲乙两个天气预报站同时预报准确的概率;
(Ⅱ)至少有一个预报站预报准确的概率;
(Ⅲ)如果甲站独立预报3次,其中恰有两次预报准确的概率 查看习题详情和答案>>
在同一时间段里,有甲乙两个天气预报站相互独立的对天气进行预测,根据以往的统计规律,甲预报站对天气预测的准确率为0.8,乙预报站对天气预测的准确率为0.75,求在同一时间段内
(Ⅰ)甲乙两个天气预报站同时预报准确的概率;
(Ⅱ)至少有一个预报站预报准确的概率;
(Ⅲ)如果甲站独立预报3次,其中恰有两次预报准确的概率
查看习题详情和答案>>
在同一时间段里,有甲乙两个天气预报站相互独立的对天气进行预测,根据以往的统计规律,甲预报站对天气预测的准确率为0.8,乙预报站对天气预测的准确率为0.75,求在同一时间段内
(Ⅰ)甲乙两个天气预报站同时预报准确的概率;
(Ⅱ)至少有一个预报站预报准确的概率;
(Ⅲ)如果甲站独立预报3次,其中恰有两次预报准确的概率
查看习题详情和答案>>
(Ⅰ)甲乙两个天气预报站同时预报准确的概率;
(Ⅱ)至少有一个预报站预报准确的概率;
(Ⅲ)如果甲站独立预报3次,其中恰有两次预报准确的概率
查看习题详情和答案>>
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为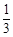 和
和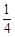 ,求(1)恰有1人译出密码的概率;
,求(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为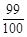 ,至少需要多少个乙这样的人?
,至少需要多少个乙这样的人?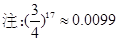
【解析】第一问中,考虑两种情况,是甲乙中的那个人译出密码,然后利用互斥事件概率公式相加得到。
第二问中,利用间接法n个乙这样的人都译不出密码的概率为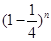 .可以得到结论。
.可以得到结论。
解:设“甲译出密码”为事件A;“乙译出密码”为事件B,则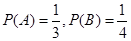 .
.
(1)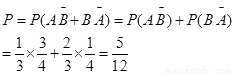 ………………5分
………………5分
(2)n个乙这样的人都译不出密码的概率为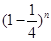 .
.
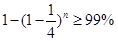 .解得.
.解得.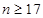
达到译出密码的概率为99/100,至少需要17人.
查看习题详情和答案>>
 某厂制造A种电子装置45台,B种电子装置55台,为了给每台装置装配一个外壳,要从两种不同规格的薄钢板上截取.已知甲种薄钢板每张面积为2m2,可做A种外壳3个和B种外壳5个;乙种薄钢板每张面积为3m2,可做A种和B种外壳各6个,用这两种薄钢板各多少张,才能使总的用料面积最小?(请根据题意,在下面的横线处按要求填上恰当的关系式或数值)
某厂制造A种电子装置45台,B种电子装置55台,为了给每台装置装配一个外壳,要从两种不同规格的薄钢板上截取.已知甲种薄钢板每张面积为2m2,可做A种外壳3个和B种外壳5个;乙种薄钢板每张面积为3m2,可做A种和B种外壳各6个,用这两种薄钢板各多少张,才能使总的用料面积最小?(请根据题意,在下面的横线处按要求填上恰当的关系式或数值)解:设用甲、乙两种薄钢板各x张,y张,
则可做A种外壳
3x+6y
3x+6y
个,B种外壳5x+6y
5x+6y
个,所用钢板的总面积为z=2x+3y
2x+3y
(m2)依题得线性约束条件为:
|
|
(5,5)
(5,5)
,且最小值zmin=25
25
(m2)