摘要:15.等差数列{an}各项均为正整数.a1=3.前n项和为Sn.等比数列{bn}中.b1=1.且b2S2=64.{ban}是公比为64的等比数列. (1)求an与bn, (2)证明:++-+<. (1)解:设{an}的公差为d.{bn}的公比为q.则d为正整数. an=3+(n-1)d.bn=qn-1. 依题意有① 由(6+d)q=64知q为正有理数.又由q=2知.d为6的因子1,2,3,6之一.解①得d=2.q=8. 故an=3+2(n-1)=2n+1.bn=8n-1. (2)证明:Sn=3+5+-+(2n+1)=n(n+2). 所以++-+=+++-+= =<.
网址:http://m.1010jiajiao.com/timu_id_4449337[举报]
(2008江西高考,文16)如图,在正六边形ABCDEF中,有下列四个命题:

A. ;
;
B. ;
;
C. ;
;
D. .
.
其中真命题的代号是_____________.(写出所有真命题的代号)
查看习题详情和答案>>
(2008•湖北模拟)数列{4an}是一个首项为4,公比为2的等比数,Sn是{an}的前n项和.
(1)求数列{an}的通项及Sn
(2)设点列Qn(
,
),n∈N+试求出一个半径最小的圆,使点列Qn中任何一个点都不在该圆外部.
查看习题详情和答案>>
(1)求数列{an}的通项及Sn
(2)设点列Qn(
| an |
| n |
| Sn |
| n2 |
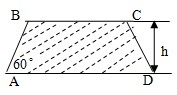 (2008•杨浦区二模)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(2008•杨浦区二模)建造一条防洪堤,其断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为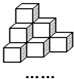 (2008•南汇区二模)将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第1层、第2层、第3层、….则第2008层正方体的个数是
(2008•南汇区二模)将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第1层、第2层、第3层、….则第2008层正方体的个数是