摘要：所以数列是首项2.公比为2的等比数列.
网址：http://m.1010jiajiao.com/timu_id_443784[举报]
已知数列
是首项为
的等比数列，且满足
.
（1） 求常数
的值和数列的通项公式；
（2） 若抽去数列中的第一项、第四项、第七项、……、第
项、……，余下的项按原来的顺序组成一个新的数列
，试写出数列的通项公式；
（3） 在（2）的条件下，设数列的前
项和为
.是否存在正整数，使得
？若存在，试求所有满足条件的正整数的值；若不存在，请说明理由.
【解析】第一问中解：由
得
，，
又因为存在常数p使得数列
为等比数列，
则
即
，所以p=1
故数列为首项是2，公比为2的等比数列，即
.
此时
也满足，则所求常数的值为1且
第二问中，解：由等比数列的性质得：
（i）当
时，
；
（ii） 当
时，
，
所以
第三问假设存在正整数n满足条件，则
，
则（i）当时，
，
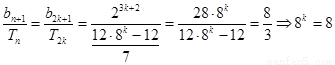
查看习题详情和答案>>
对于数列{un}，若存在常数M＞0，对任意的（n∈N*），恒有|un+1-u|+|un+un-1|+…+|u2-u1|≤M，则称数列{un}为B-数列．
（1）首项为1，公比为-
的等比数列是否为B-数列？请说明理由；
（2）设{sn}是数列{xn}的前n项和．给出下列两组判断：
A组：①数列{xn}是B-数列，②数列{xn}不是B-数列；
B组：③数列{sn}是B-数列，④数列{sn}不是B-数列．
请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题．判断所给命题的真假，并证明你的结论． 查看习题详情和答案>>
（1）首项为1，公比为-
| 1 | 2 |
（2）设{sn}是数列{xn}的前n项和．给出下列两组判断：
A组：①数列{xn}是B-数列，②数列{xn}不是B-数列；
B组：③数列{sn}是B-数列，④数列{sn}不是B-数列．
请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题．判断所给命题的真假，并证明你的结论． 查看习题详情和答案>>
对于数列{un}若存在常数M＞0，对任意的n∈N*，恒有|un+1-un|+|un-un-1|+…+|u2-u1|≤M，则称数列{un}为B-数列。
（1）首项为1，公比为q（|q|＜1）的等比数列是否为B-数列？请说明理由；
请以其中一组的一个论断条件，另一组中的一个论断为结论组成一个命题，判断所给命题的真假，并证明你的结论；
（2）设Sn是数列{xn}的前n项和，给出下列两组论断；
A组：①数列{xn}是B-数列②数列{xn}不是B-数列
B组：③数列{Sn}是B-数列④数列{Sn}不是B-数列
请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题。判断所给命题的真假，并证明你的结论；
（3）若数列{an}，{bn}都是B-数列，证明：数列{anbn}也是B-数列。
查看习题详情和答案>>
（1）首项为1，公比为q（|q|＜1）的等比数列是否为B-数列？请说明理由；
请以其中一组的一个论断条件，另一组中的一个论断为结论组成一个命题，判断所给命题的真假，并证明你的结论；
（2）设Sn是数列{xn}的前n项和，给出下列两组论断；
A组：①数列{xn}是B-数列②数列{xn}不是B-数列
B组：③数列{Sn}是B-数列④数列{Sn}不是B-数列
请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题。判断所给命题的真假，并证明你的结论；
（3）若数列{an}，{bn}都是B-数列，证明：数列{anbn}也是B-数列。
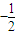的等比数列是否为B-数列？请说明理由；
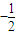的等比数列是否为B-数列？请说明理由；