摘要:17 设的内角..的对边长分别为.... .求. 18 如图.直三棱柱中..分别为.的中点. 平面 (I)证明: (II)设二面角为60°.求与平面所成的角的大小. 19 设数列的前项和为 已知 (I)设.证明数列是等比数列 (II)求数列的通项公式. 20 某车间甲组有10名工人.其中有4名女工人,乙组有5名工人.其中有3名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲.乙两组中共抽取3名工人进行技术考核. (I)求从甲.乙两组各抽取的人数, (II)求从甲组抽取的工人中恰有1名女工人的概率, (III)记表示抽取的3名工人中男工人数.求的分布列及数学期望. 已知椭圆的离心率为.过右焦点F的直线与相交于.粮店.当的斜率为1时.坐标原点到的距离为 (I)求.的值, (II)上是否存在点P.使得当绕F转到某一位置时.有成立? 若存在.求出所有的P的坐标与的方程,若不存在.说明理由.22. 设函数有两个极值点.且 (I)求的取值范围.并讨论的单调性, (II)证明:
网址:http://m.1010jiajiao.com/timu_id_4431395[举报]
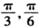 (单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中
(单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中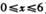 ),
),
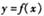 的函数解析式;
的函数解析式;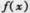 图象上的各点均向右平移2个单位长度,得到
图象上的各点均向右平移2个单位长度,得到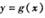 的图象,求函数
的图象,求函数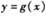 的单调递减区间.
的单调递减区间.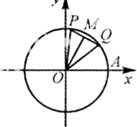
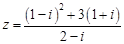 ,若
,若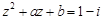 ,
,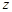 ;
;
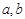 的值
的值 ,向量
,向量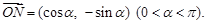
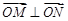 ,求
,求 的值;
的值;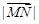 的最大值及此时
的最大值及此时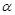 的值。
的值。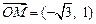 ,向量
,向量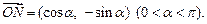
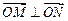 ,求
,求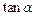 的值;
的值;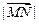 的最大值及此时
的最大值及此时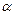 的值。
的值。