摘要:20. [解]:(1)当时. ---- 当时..在内单调递增, 当时.恒成立.故在内单调递增, 的单调增区间为. ---- (2)①当时.. .恒成立.在上增函数. 故当时.. ----8分) ②当时.. (Ⅰ)当.即时.在时为正数.所以在区间上为增函数.故当时..且此时 ---- (Ⅱ)当.即时.在时为负数.在时为正数.所以在区间上为减函数.在上为增函数.故当时..且此时. ---- (Ⅲ)当.即时.在进为负数.所以在区间上为减函数.故当时.. ---- 所以函数的最小值为. 由条件得此时,或.此时,或.此时无解. 综上.. ---- 数学Ⅱ
网址:http://m.1010jiajiao.com/timu_id_4430364[举报]
已知函数 ,(
,( ),
),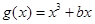
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令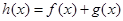 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,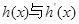 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当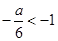 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。
查看习题详情和答案>>
已知函数
 ;
;
(1)若函数 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数 的取值范围。
的取值范围。
(2)若函数 ,若在[1,e]上至少存在一个x的值使
,若在[1,e]上至少存在一个x的值使 成立,求实数
成立,求实数 的取值范围。
的取值范围。
【解析】第一问中,利用导数 ,因为
,因为 在其定义域内的单调递增函数,所以
在其定义域内的单调递增函数,所以 内满足
内满足 恒成立,得到结论第二问中,在[1,e]上至少存在一个x的值使
恒成立,得到结论第二问中,在[1,e]上至少存在一个x的值使 成立,等价于不等式
成立,等价于不等式 在[1,e]上有解,转换为不等式有解来解答即可。
在[1,e]上有解,转换为不等式有解来解答即可。
解:(1) ,
,
因为 在其定义域内的单调递增函数,
在其定义域内的单调递增函数,
所以 内满足
内满足 恒成立,即
恒成立,即 恒成立,
恒成立,
亦即 ,
,
 即可 又
即可 又
当且仅当 ,即x=1时取等号,
,即x=1时取等号,
 在其定义域内为单调增函数的实数k的取值范围是
在其定义域内为单调增函数的实数k的取值范围是 .
.
(2)在[1,e]上至少存在一个x的值使 成立,等价于不等式
成立,等价于不等式 在[1,e]上有解,设
在[1,e]上有解,设

 上的增函数,
上的增函数, 依题意需
依题意需
 实数k的取值范围是
实数k的取值范围是
查看习题详情和答案>>



