摘要:求差法:a>b a-b>0
网址:http://m.1010jiajiao.com/timu_id_4430033[举报]
已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|)
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x0<x1<…<xi<…<xn=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
|m(xi)-m(xi-1)|≤M恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
f(x)=f(x1)+f(x2)+…+f(xn))
查看习题详情和答案>>
(Ⅰ)求实数a,b的值;
(Ⅱ)若不等式f(log2k)>f(2)成立,求实数k的取值范围;
(Ⅲ)定义在[p,q]上的一个函数m(x),用分法T:p=x0<x1<…<xi<…<xn=q将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
| n |
 |
| i=1 |
| n |
 |
| i=1 |
有编号01~12的12种食品,它们微量元素A的含量依次是:42、45、a、b、85、94、100、108、133、138、150、175(其中45<a<b<85),平均含量和方差分别是100、1656.
①求a、b;
②按编号用系统抽样法从以上12种食品中随机地抽4种分析微量元素B,求06号食品被抽中的概率;
③如果微量元素B与微量元素A具有线性相关关系,②抽样所得样本中,哪个样本用来分析微量元素B更有代表性?
(参考数值:(42-100)2+(45-100)2+(85-100)2+(94-100)2+(100-100)2+(108-100)2+(133-100)2+(138-100)2+(150-100)2+(175-100)2=17372) 查看习题详情和答案>>
①求a、b;
②按编号用系统抽样法从以上12种食品中随机地抽4种分析微量元素B,求06号食品被抽中的概率;
③如果微量元素B与微量元素A具有线性相关关系,②抽样所得样本中,哪个样本用来分析微量元素B更有代表性?
(参考数值:(42-100)2+(45-100)2+(85-100)2+(94-100)2+(100-100)2+(108-100)2+(133-100)2+(138-100)2+(150-100)2+(175-100)2=17372) 查看习题详情和答案>>
已知一条曲线C在y轴右边,C上任意一点到点F1(2,0)的距离减去它到y轴距离的差都是2.
(1)求曲线C的方程;
(2)若双曲线M:x2-
=1(t>0)的一个焦点为F1,另一个焦点为2,过F2的直线l与M相交于A、B两点,直线l的法向量为
=(k,-1)(k>0),且
•
=0,求k的值.
查看习题详情和答案>>
(1)求曲线C的方程;
(2)若双曲线M:x2-
| y2 |
| t |
| n |
| OA |
| OB |
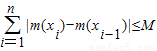 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: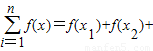 …+f(xn))
…+f(xn))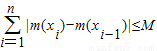 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: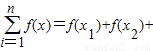 …+f(xn))
…+f(xn))