摘要:命题的定义:可以判断真假的语句叫做命题.
网址:http://m.1010jiajiao.com/timu_id_4429339[举报]
(2012•自贡三模)对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f′(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
①任意三次函数都关于点(-
,f(-
))对称:
②存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为函数y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)=
x3-
x2-
,则,g(
)+g(
)+g(
)+…+g(
)=-105.5.
其中正确命题的序号为
查看习题详情和答案>>
①任意三次函数都关于点(-
| b |
| 3a |
| b |
| 3a |
②存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为函数y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2012 |
| 2 |
| 2012 |
| 3 |
| 2012 |
| 2011 |
| 2012 |
其中正确命题的序号为
①②④
①②④
(把所有正确命题的序号都填上).
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f′(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f′(x)=0有实数解x,则称点(x,f(x))为函数y=f(x)的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
①任意三次函数都关于点(- ,f(-
,f(- ))对称:
))对称:
②存在三次函数f′(x)=0有实数解x,点(x,f(x))为麵y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)= x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g( )+…+g(
)+…+g( )=-105.5.
)=-105.5.
其中正确命题的序号为 (把所有正确命题的序号都填上). 查看习题详情和答案>>
①任意三次函数都关于点(-
 ,f(-
,f(- ))对称:
))对称:②存在三次函数f′(x)=0有实数解x,点(x,f(x))为麵y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)=
 x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g( )+…+g(
)+…+g( )=-105.5.
)=-105.5.其中正确命题的序号为 (把所有正确命题的序号都填上). 查看习题详情和答案>>
对于三次函数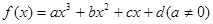 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数都关于点 对称:
对称:
②存在三次函数 有实数解
有实数解 ,点
,点 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则,
,则,
其中正确命题的序号为__ _____(把所有正确命题的序号都填上).
查看习题详情和答案>>
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f′(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f′(x)=0有实数解x,则称点(x,f(x))为函数y=f(x)的“拐点”,可以发现,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一发现判断下列命题:
①任意三次函数都关于点(- ,f(-
,f(- ))对称:
))对称:
②存在三次函数f′(x)=0有实数解x,点(x,f(x))为麵y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)= x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g(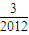 )+…+g(
)+…+g( )=-105.5.
)=-105.5.
其中正确命题的序号为 (把所有正确命题的序号都填上). 查看习题详情和答案>>
①任意三次函数都关于点(-
 ,f(-
,f(- ))对称:
))对称:②存在三次函数f′(x)=0有实数解x,点(x,f(x))为麵y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)=
 x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g(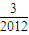 )+…+g(
)+…+g( )=-105.5.
)=-105.5.其中正确命题的序号为 (把所有正确命题的序号都填上). 查看习题详情和答案>>
 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点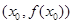 为函数
为函数 对称:
对称: 有实数解
有实数解 为函数
为函数 ,则,
,则,