摘要:组合数的两个性质: (1) = ; (2) += (3).
网址:http://m.1010jiajiao.com/timu_id_4427253[举报]
规定
且
(1)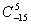 的值;
的值;
(2)组合数的两个性质: ;
; 是否都能推广到
是否都能推广到 的情形?若能推广,则写出推广的形式并给予证明,或不能则说明理由;
的情形?若能推广,则写出推广的形式并给予证明,或不能则说明理由;
(3)已知组合数 是正整数,证明:当
是正整数,证明:当 是正整数时,
是正整数时, 。
。
查看习题详情和答案>>
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数: ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数:
 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意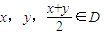 均满足
均满足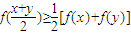 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数: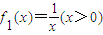 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
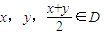 均满足
均满足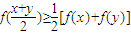 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)大小.
(2)给定两个函数:
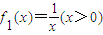 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.(3)试利用(2)的结论解决下列问题:若实数m、n满足2m+2n=1,求m+n的最大值.
查看习题详情和答案>>
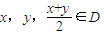 均满足
均满足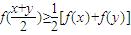 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.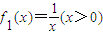 ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.