摘要：画出函数y=x及y=的图象.并且说明这两个函数的相同性质和不同性质. 解:相同性质:两图象都位于y轴右方.都经过点(1.0).这说明两函数的定义域都是.且当x=1,y=0. 不同性质:y=x的图象是上升的曲线.y=的图象是下降的曲线.这说明前者在上是增函数.后者在上是减函数.
网址：http://m.1010jiajiao.com/timu_id_4425676[举报]
已知y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x-x2．
（1）求y=f（x）的解析式；
（2）画出函数y=f（x）的图象，并指出f（x）的单调区间及在每个区间上的增减性；
（3）若函数y=f（x）的定义域为[a，b]，值域为[
，
] (1≤a＜b)，求实数a、b的值．
查看习题详情和答案>>
（1）求y=f（x）的解析式；
（2）画出函数y=f（x）的图象，并指出f（x）的单调区间及在每个区间上的增减性；
（3）若函数y=f（x）的定义域为[a，b]，值域为[
| 1 |
| b |
| 1 |
| a |
已知y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x-x2．
（1）求y=f（x）的解析式；
（2）画出函数y=f（x）的图象，并指出f（x）的单调区间及在每个区间上的增减性；
（3）若函数y=f（x）的定义域为[a，b]，值域为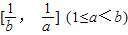
，求实数a、b的值．
查看习题详情和答案>>
（1）求y=f（x）的解析式；
（2）画出函数y=f（x）的图象，并指出f（x）的单调区间及在每个区间上的增减性；
（3）若函数y=f（x）的定义域为[a，b]，值域为
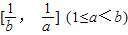，求实数a、b的值．查看习题详情和答案>>
已知函数f（x）=2sinx（sinx+cosx）-1（1）求：函数f（x）的最大值及取得最大值时的x值；
（2）在给出的直角坐标系中，用五点作图法画出函数y=f（x）一个周期内的图象
| x | |||||
| y |
已知y=f（x）是定义在R上的函数，对于任意的x∈R，f（-x）+f（x）=0，且当x＞0时，f（x）=-x2+2x+1．
已知y=f（x）是定义在R上的函数，对于任意的x∈R，f（-x）+f（x）=0，且当x≥0 时，f（x）=2x-x2．