摘要：例1 (1)已知.求x(精确到) 解:在区间上是增函数.符合条件的角是唯一的 (2)已知且.求x的取值集合 解: 所求的x的集合是(即) (3)已知.求x的取值集合 解:由上题可知:. 合并为 例2已知.根据所给范围求: 1°为锐角 2°为某三角形内角 3°为第二象限角 4° 解:1°由题设 2°设.或 3° 4°由题设 例3 求适合下列关系的x的集合 1° 2° 3° 解:1° 所求集合为 2°所求集合为 3° 例4 直角锐角A.B满足: 解:由已知: 为锐角. 例5 1°用反三角函数表示中的角x 2°用反三角函数表示中的角x 解:1° ∵ ∴ 又由 得 ∴ ∴ 2° ∵ ∴ 又由 得 ∴ ∴ 例6已知.求角x的集合 解:∵ ∴ 由 得 由 得 故角x的集合为 例7求的值 解:arctan2 = a, arctan3 = b 则tana = 2. tanb = 3 且. ∴ 而 ∴a + b = 又arctan1 = ∴= p 例8求y = arccos(sinx), ()的值域 解:设u = sin x ∵ ∴ ∴ ∴所求函数的值域为
网址：http://m.1010jiajiao.com/timu_id_4424093[举报]
（1）已知：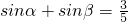
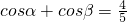求cos（α-β）的值
（2）将（1）中已知条件进行适当改变，能否求出sin（α-β）的值，若能求出其值，若不能请说明理由．
（3）你能依此也创设一道类似题吗？或将本例推广到一般情形．
查看习题详情和答案>>
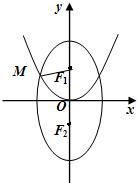与向量、圆交汇．例5：已知F1、F2分别为椭圆C1：| y2 |
| a2 |
| x2 |
| b2 |
| 5 |
| 3 |
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
| AP |
| PB |
| AQ |
| QB |
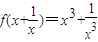，求f（x）．
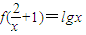，求f（x）．
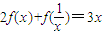，求f（x）．
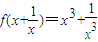，求f（x）．
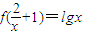，求f（x）．
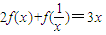，求f（x）．