题目内容
例2、(1)已知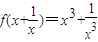 ,求f(x).
,求f(x).(2)已知
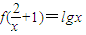 ,求f(x).
,求f(x).(3)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x).
(4)已知f(x)满足
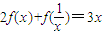 ,求f(x).
,求f(x).
【答案】分析:(1)用配凑法根据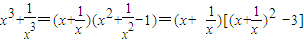 可得答案.
可得答案.
(2)用换元法,令t=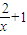 ,可得x=
,可得x=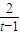 ,代入即可.
,代入即可.
(3)设f(x)=ax+b代入可得.
(4)通过联立方程组可得答案.
解答:解:(1)∵ ,
,
∴f(x)=x3-3x(x≥2或x≤-2).
(2)令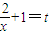 (t>1),
(t>1),
则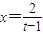 ,∴
,∴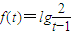 ,∴
,∴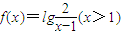 .
.
(3)设f(x)=ax+b(a≠0),
则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+b+5a=2x+17,
∴a=2,b=7,∴f(x)=2x+7.
(4)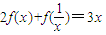 ①,把①中的x换成
①,把①中的x换成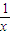 ,得
,得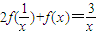 ②,
②,
①×2-②得 ,∴
,∴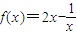 .
.
点评:本题主要考查求函数解析式的一般方法--配凑法、换元法、待定系数法、方程组法.
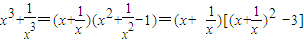 可得答案.
可得答案.(2)用换元法,令t=
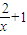 ,可得x=
,可得x=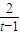 ,代入即可.
,代入即可.(3)设f(x)=ax+b代入可得.
(4)通过联立方程组可得答案.
解答:解:(1)∵
 ,
,∴f(x)=x3-3x(x≥2或x≤-2).
(2)令
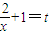 (t>1),
(t>1),则
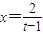 ,∴
,∴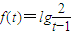 ,∴
,∴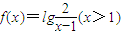 .
.(3)设f(x)=ax+b(a≠0),
则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+b+5a=2x+17,
∴a=2,b=7,∴f(x)=2x+7.
(4)
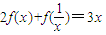 ①,把①中的x换成
①,把①中的x换成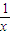 ,得
,得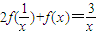 ②,
②,①×2-②得
 ,∴
,∴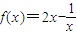 .
.点评:本题主要考查求函数解析式的一般方法--配凑法、换元法、待定系数法、方程组法.

练习册系列答案
相关题目
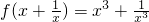 ,求f(x).
,求f(x).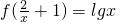 ,求f(x).
,求f(x).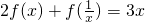 ,求f(x).
,求f(x). ,求f(x).
,求f(x). ,求f(x).
,求f(x). ,求f(x).
,求f(x).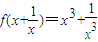 ,求f(x).
,求f(x).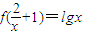 ,求f(x).
,求f(x).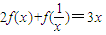 ,求f(x).
,求f(x).