摘要:14.已知平面α∥β.在α内有4个点.在β内有6个点. (1)过这10个点中的3点作一平面.最多可作多少个不同平面? (2)以这些点为顶点.最多可作多少个三棱锥? (3)上述三棱锥中最多可以有多少个不同的体积? 解:(1)所作出的平面有三类:①α内1点.β内2点确定的平面.有C·C个,②α内2点.β内1点确定的平面.有C·C个,③α.β本身. ∴所作的平面最多有C·C+C·C+2=98(个). (2)所作的三棱锥有三类:①α内1点.β内3点确定的三棱锥.有C·C个,②α内2点.β内2点确定的三棱锥.有C·C个,③α内3点.β内1点确定的三棱锥.有C·C个. ∴最多可作出的三棱锥有: C·C+C·C+C·C=194(个) (3)∵当等底面积.等高的情况下三棱锥的体积相等. 且平面α∥β.∴体积不相同的三棱锥最多有 C+C+C·C=114(个)
网址:http://m.1010jiajiao.com/timu_id_4422823[举报]
已知平面![]() ∥
∥![]() ,在
,在![]() 内有4个点,在
内有4个点,在![]() 内有6个点.
内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
查看习题详情和答案>>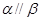 ,在
,在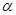 内有4个点,在
内有4个点,在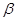 内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.
内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.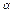 ∥
∥ ,在
,在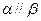 ,在
,在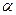 内有4个点,在
内有4个点,在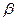 内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.
内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.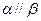 ,在
,在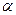 内有4个点,在
内有4个点,在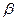 内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.
内有6个点,以这些点为顶点,最多可作 个三棱锥,在这些三棱锥中最多可以有 个不同的体积.