摘要： 证明:(1)① . ································ 3分 ②由得. 分别是的中点.················ 4分 又 .即为等腰三角形···················· 6分 中的两个结论仍然成立．······················ 8分 (3)在图②中正确画出线段 由(1)同理可证 又 .和都是顶角相等的等腰三角形··········· 10分 . 12分
网址：http://m.1010jiajiao.com/timu_id_4421061[举报]
如图，
是
的两条切线，切点分别为
，连结
，在
外作
，
交
的延长线于点
．
(1
）在图中找出一对全等三角形，并进行证明；(2
）如果
的半径为3，
，试求切线
的长；
(3
）试说明：
分别是由
，
经过哪种变换得到的（直接写出结果）．
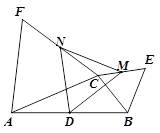
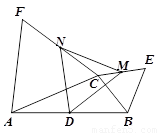
如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形， M、N分别是CE、CF的中点.
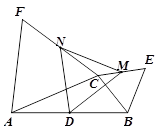
1.求证：△DMN是等边三角形；
2.连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.
同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：
小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.
查看习题详情和答案>>
如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形， M、N分别是CE、CF的中点.
【小题1】求证：△DMN是等边三角形；
【小题2】连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.
同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：
小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置. 查看习题详情和答案>>
【小题1】求证：△DMN是等边三角形；
【小题2】连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.
同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：
小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置. 查看习题详情和答案>>
