摘要:1.三角函数的性质:(结合图象理解, 表中)) y=sinx y=cosx y=tanx y=cotx 定义域 R R {x∈R|x≠kπ} 值域 [-1,1] [-1,1] R R 周期 2π 2π π π 奇偶性 奇函数 偶函数 奇函数 奇函数 增区间 无 减区间 无 对称轴 x=kπ 无 对称 中心 (,0)
网址:http://m.1010jiajiao.com/timu_id_4420711[举报]
已知函数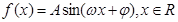 (其中
(其中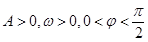 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为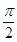 ,且图象上一个最低点为
,且图象上一个最低点为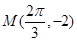 .
.
(1)求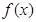 的解析式; (2)当
的解析式; (2)当 ,求
,求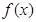 的值域.
的值域.
【解析】第一问利用三角函数的性质得到)由最低点为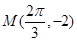 得A=2. 由x轴上相邻的两个交点之间的距离为
得A=2. 由x轴上相邻的两个交点之间的距离为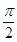 得
得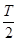 =
=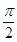 ,即
,即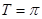 ,
,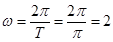 由点
由点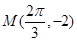 在图像上的
在图像上的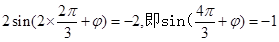
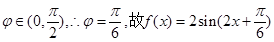
第二问中,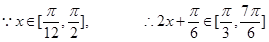

当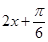 =
=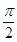 ,即
,即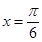 时,
时,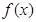 取得最大值2;当
取得最大值2;当
即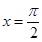 时,
时,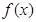 取得最小值-1,故
取得最小值-1,故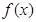 的值域为[-1,2]
的值域为[-1,2]
查看习题详情和答案>>
已知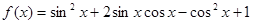
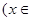 R
R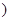 .
.
(1)求函数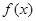 的最大值,并指出此时
的最大值,并指出此时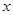 的值.
的值.
(2)若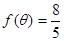 ,求
,求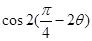 的值.
的值.
【解析】本试题主要考查了三角函数的性质的运用。(1)中,三角函数先化简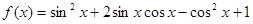 =
=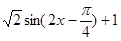 ,然后利用
,然后利用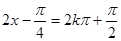 是,函数取得最大值
是,函数取得最大值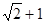 (2)中,结合(1)中的结论,然后由
(2)中,结合(1)中的结论,然后由
得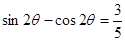 ,两边平方得
,两边平方得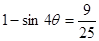 即
即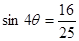 ,因此
,因此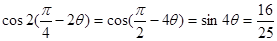
查看习题详情和答案>>
已知 中,内角
中,内角 的对边的边长分别为
的对边的边长分别为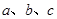 ,且
,且
(I)求角 的大小;
的大小;
(II)若 求
求 的最小值.
的最小值.
【解析】第一问,由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
第二问,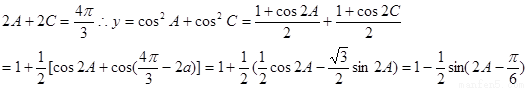
三角函数的性质运用。
解:(Ⅰ)由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
(Ⅱ)由(Ⅰ)可知
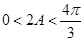 ,
, ,则当
,则当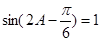 ,即
,即 时,y的最小值为
时,y的最小值为 .
.
查看习题详情和答案>>
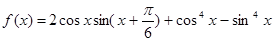
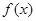 的最小正周期;
的最小正周期;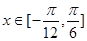 ,求
,求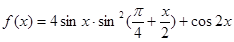 ,
,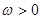 ,若
,若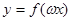 在区间
在区间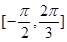 上是增函数,求
上是增函数,求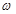 的取值范围;
的取值范围;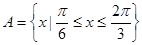 ,
,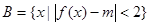 ,若
,若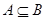 ,求
,求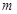 的取值范围.
的取值范围.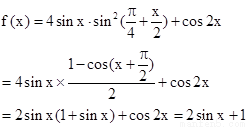
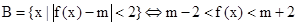 解得参数m的取值范围。
解得参数m的取值范围。