摘要： 已知等比数列的各项不为1的正数,数列满足(且 ),设,. (I)求数列的前多少项和最大,最大值是多少? (II)设,,求的值. (III)试判断,是否存在自然数M,使当时恒成立,若存在求出相应的M;若不存 在,请说明理由. 15设函数的定义域为全体实数,对于任意不相等的实数,,都有 ,且存在,使得,数列中,,, 求证:对于任意的自然数,有: (I); (II).
网址：http://m.1010jiajiao.com/timu_id_4420466[举报]
（14分）已知等比数列
的各项均为正数，且公比不等于1，数列
对任意正整数n，均有：
成立，又
。
（Ⅰ）求数列的通项公式及前n项和
；
（Ⅱ）在数列中依次取出第1项，第2项，第4项，第8项，……，第
项，……，组成一个新数列
，求数列的前n项和
；
（Ⅲ）当
时，比较与的大小。
}的各项为不等于1的正数，数列{
}的通项公式为
，其中1＜a＜
为常数，对于k 、t∈N，k≠t ，满足
， 
，是否存在自然数
使得n＞
＞1恒成 立？ 若存在求出相应的
的各项为不等于1的正数，数列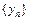
满足
，设
。
，
，求
的值.
的各项为不等于1的正数，数列
满足
，设
。
，
，求
的值.
的各项为均不等于1的正数，数列
满足
则数列
的前n项和的最大值等于 （ ）高考资源网