摘要：19．(1)已知.证明不存在实数能使等式cos+msin=m(*)成立, (2)试扩大的取值范围.使对于实数.等式(*)能成立, (3)在扩大后的取值范围内.若取,求出使等式(*)成立的值. 提示:(1)可化为(2)(3)
网址：http://m.1010jiajiao.com/timu_id_4420365[举报]
已知f（x）=xlnx．
（1）求g（x）=
（k∈R）的单调区间；
（2）证明：当x≥1时，2x-e≤f（x）≤
恒成立；
（3）任取两个不相等的正数x1，x2，且x1＜x2，若存x0＞0使f′（x0）=
成立，证明：x0＞x1．
查看习题详情和答案>>
（1）求g（x）=
| f(x)+k |
| x |
（2）证明：当x≥1时，2x-e≤f（x）≤
| x2-1 |
| 2 |
（3）任取两个不相等的正数x1，x2，且x1＜x2，若存x0＞0使f′（x0）=
| f(x1)-f(x2) |
| x1-x2 |
已知f（x）=xlnx．
（1）求g（x）=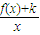
（k∈R）的单调区间；
（2）证明：当x≥1时，2x-e≤f（x）≤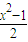
恒成立；
（3）任取两个不相等的正数x1，x2，且x1＜x2，若存x＞0使f′（x）=
成立，证明：x＞x1．
查看习题详情和答案>>
（1）求g（x）=
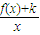（k∈R）的单调区间；（2）证明：当x≥1时，2x-e≤f（x）≤
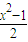恒成立；（3）任取两个不相等的正数x1，x2，且x1＜x2，若存x＞0使f′（x）=
成立，证明：x＞x1．查看习题详情和答案>>
已知函数
．
（I)若
，是否存在a，b
R，y＝f（x）为偶函数．如果存
在．请举例并证明你的结论，如果不存在，请说明理由；
〔II）若a＝2，b＝1．求函数
在R上的单调区间；
（III )对于给定的实数
成立．求a的取值范围．
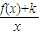（k∈R）的单调区间；
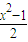恒成立；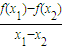
成立，证明：x＞x1．
．