摘要:4.若是奇函数.且当>0时..则当时.为( C ) (A) (B) (C)|| (D)||
网址:http://m.1010jiajiao.com/timu_id_4420350[举报]
(2012•保定一模)已知函数f(x)=x2-2x,g(x)是R上的奇函数,且当x∈(-∞,0],g(x)+f(x)=x2.
(1)求函数g(x)在R上的解析式;
(2)若函数h(x)=x[g(x)-λf(x)+
]在〔0,+∞)上是增函数,且λ≤0,求λ的取值范围.
查看习题详情和答案>>
(1)求函数g(x)在R上的解析式;
(2)若函数h(x)=x[g(x)-λf(x)+
| 2 | 3 |
(A类)定义在R上的函数y=f(x),对任意的a,b∈R,满足f(a+b)=f(a)•f(b),当x>0时,有f(x)>1,其中f(1)=2
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数f(x)=
.
(1)求a,b的值;
(2)若不等式-m2+(k+2)m-
<f(x)<m2+2km+k+
对一切实数x及m恒成立,求实数k的取值范围;
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.
查看习题详情和答案>>
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数f(x)=
| -2x+b |
| 2x+1+a |
(1)求a,b的值;
(2)若不等式-m2+(k+2)m-
| 3 |
| 2 |
| 5 |
| 2 |
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.
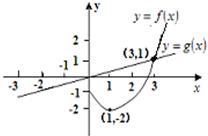 对于任意的实数a,b,记max{a,b}=
对于任意的实数a,b,记max{a,b}=
|
| A、y=F(x)为奇函数 |
| B、y=F(x)在(-3,0)上为增函数 |
| C、y=F(x)的最小值为-2,最大值为2 |
| D、以上说法都不正确 |