题目内容
(A类)定义在R上的函数y=f(x),对任意的a,b∈R,满足f(a+b)=f(a)•f(b),当x>0时,有f(x)>1,其中f(1)=2
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数f(x)=
.
(1)求a,b的值;
(2)若不等式-m2+(k+2)m-
<f(x)<m2+2km+k+
对一切实数x及m恒成立,求实数k的取值范围;
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.
(1)求f(0)、f(-1)的值; (2)证明y=f(x)在(0,+∞)上是增函数;(3)求不等式f(x+1)<4的解集.
(B类)已知定义在R上的奇函数f(x)=
| -2x+b |
| 2x+1+a |
(1)求a,b的值;
(2)若不等式-m2+(k+2)m-
| 3 |
| 2 |
| 5 |
| 2 |
(3)定义:若存在一个非零常数T,使得f(x+T)=f(x)对定义域中的任何实数x都恒成立,那么,我们把f(x)叫以T为周期的周期函数,它特别有性质:对定义域中的任意x,f(x+nT)=f(x),(n∈Z).若函数g(x0是定义在R上的周期为2的奇函数,且当x∈(-1,1)时,g(x)=f(x)-x,求方程g(x)=0的所有解.
分析:A类
(1)令a=1,b=0,则有:f(1)=f(1)•f(0),结合已知得出f(0)=1.再令a=1,b=-1 可以得出f(-1)=
.
(2)任意x1,x2∈(0,+∞),且x1<x2,则f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x2-x1)•f(x1)-f(x1)=f(x1)(f(x2-x1)-1)由已知,可以判断出差为正数.
(3)考虑利用函数的单调性求解,注意x+1的取值范围,进行分类讨论.
B类
(1)由f(0)=0,得b=1,f(-1)=-f(1),得a=2 由f(x)=
=-
+
得出-
<f(x)<
转化为
对m∈R恒成立,进行解决.
(3)利用函数单调性在(-1,1)内,g(x)=0有唯一的根x=0,再由g(-1)=g(-1+2)得-g(1)=g(1),g(1)=0,结合周期性求出所有的解.
(1)令a=1,b=0,则有:f(1)=f(1)•f(0),结合已知得出f(0)=1.再令a=1,b=-1 可以得出f(-1)=
| 1 |
| 2 |
(2)任意x1,x2∈(0,+∞),且x1<x2,则f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x2-x1)•f(x1)-f(x1)=f(x1)(f(x2-x1)-1)由已知,可以判断出差为正数.
(3)考虑利用函数的单调性求解,注意x+1的取值范围,进行分类讨论.
B类
(1)由f(0)=0,得b=1,f(-1)=-f(1),得a=2 由f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2 |
| 1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
|
(3)利用函数单调性在(-1,1)内,g(x)=0有唯一的根x=0,再由g(-1)=g(-1+2)得-g(1)=g(1),g(1)=0,结合周期性求出所有的解.
解答:A类
解:(1)在f(a+b)=f(a)•f(b)中
令a=1,b=0,则有:f(1)=f(1)•f(0)
因为当x>0时,有f(x)>1,所以f(1)>1,∴f(0)=1 …(2分)
令a=1,b=-1,则f(0)=f(1)•f(-1),得出f(-1)=
=
…(4分)
(2)任意x1,x2∈(0,+∞),且x1<x2,则f(x2)-f(x1)=f(x2-x1+x1)-f(x1)
=f(x2-x1)•f(x1)-f(x1)=f(x1)(f(x2-x1)-1).
由于0<x1<x2,所以f(x1)>1,f(x2-x1)-1>0
所以f(x2)-f(x1)>0,f(x2)>f(x1).
y=f(x)在(0,+∞)上是增函数.…(8分)
(3)∵f(1)=2
∴f(2)=f(1)•f(1)=4
由已知,当x<0时,
f(0)=f(x)f(-x)=1,得出f(x)=
<1.…(10分)
故①.当x+1<0即x<-1时,f(x+1)<1<4不等式恒成立. …(11分)
②.当x+1=0即x=-1时,f(x+1)=1<4 …(12分)
③.当x+1>0即x>-1时,由(2)知道须x+1<2,解得-1<x<1 …(13分)
综上:不等式f(x+1)<4的解集为{x|x<1}.…(14分)
B类:
解:(1)由f(0)=0,得b=1,f(-1)=-f(1),得a=2
(2)f(x)=
=-
+
得出-
<f(x)<
…(5分)
即
对m∈R恒成立,即
对m∈R恒成立 …(7分)
∴
…(9分)
解得-1≤k≤0 …(10分)
(3)x∈(-1,1),而g(x)=f(x)-x=-
+
-x在(-1,1)内单减.
且g(0)=0,故在(-1,1)内,g(x)=0有唯一的根x=0,又g(x)周期为2,对k∈Z,
g(x+2k)=g(x),所以在(2k-1,2k+1)内有唯一根x=2k
由g(-1)=g(-1+2)得-g(1)=g(1),g(1)=0
应有g(2k+1)=0,即还有解x=2k+1,
综上:g(x)=0 的所有解为x=k(k∈Z)
解:(1)在f(a+b)=f(a)•f(b)中
令a=1,b=0,则有:f(1)=f(1)•f(0)
因为当x>0时,有f(x)>1,所以f(1)>1,∴f(0)=1 …(2分)
令a=1,b=-1,则f(0)=f(1)•f(-1),得出f(-1)=
| f(0) |
| f(1) |
| 1 |
| 2 |
(2)任意x1,x2∈(0,+∞),且x1<x2,则f(x2)-f(x1)=f(x2-x1+x1)-f(x1)
=f(x2-x1)•f(x1)-f(x1)=f(x1)(f(x2-x1)-1).
由于0<x1<x2,所以f(x1)>1,f(x2-x1)-1>0
所以f(x2)-f(x1)>0,f(x2)>f(x1).
y=f(x)在(0,+∞)上是增函数.…(8分)
(3)∵f(1)=2
∴f(2)=f(1)•f(1)=4
由已知,当x<0时,
f(0)=f(x)f(-x)=1,得出f(x)=
| 1 |
| f(-x) |
故①.当x+1<0即x<-1时,f(x+1)<1<4不等式恒成立. …(11分)
②.当x+1=0即x=-1时,f(x+1)=1<4 …(12分)
③.当x+1>0即x>-1时,由(2)知道须x+1<2,解得-1<x<1 …(13分)
综上:不等式f(x+1)<4的解集为{x|x<1}.…(14分)
B类:
解:(1)由f(0)=0,得b=1,f(-1)=-f(1),得a=2
(2)f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2 |
| 1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
即
|
|
∴
|
解得-1≤k≤0 …(10分)
(3)x∈(-1,1),而g(x)=f(x)-x=-
| 1 |
| 2 |
| 1 |
| 2x+1 |
且g(0)=0,故在(-1,1)内,g(x)=0有唯一的根x=0,又g(x)周期为2,对k∈Z,
g(x+2k)=g(x),所以在(2k-1,2k+1)内有唯一根x=2k
由g(-1)=g(-1+2)得-g(1)=g(1),g(1)=0
应有g(2k+1)=0,即还有解x=2k+1,
综上:g(x)=0 的所有解为x=k(k∈Z)
点评:A类 本题考查抽象函数、单调性的判定、及单调性的应用,考查转化、分类讨论的思想方法.牢牢把握所给的关系式,对式子中的字母准确灵活的赋值,变形构造是解决抽象函数问题常用的思路.
B类 考查了函数的奇偶性、单调性、周期性,不等式恒成立问题,以及方程思想,考查计算、转化能力.
B类 考查了函数的奇偶性、单调性、周期性,不等式恒成立问题,以及方程思想,考查计算、转化能力.

练习册系列答案
相关题目
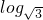 (x+a)的图象上.
(x+a)的图象上.