摘要:41.在圆中.注意利用半径.半弦长.及弦心距组成的直角三角形.
网址:http://m.1010jiajiao.com/timu_id_4419516[举报]
已知椭圆C:
+
=1,(a>b>0)的两焦点分别为F1、F2,|F1F2|=4
,离心率e=
.过直线l:x=
上任意一点M,引椭圆C的两条切线,切点为A、B.
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x0,y0)处的切线方程为:x0x+y0y=r2”.由上述结论类比得到:“过椭圆
+
=1(a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(2)利用(1)中的结论证明直线AB恒过定点(2
,0);
(3)当点M的纵坐标为1时,求△ABM的面积. 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
2
| ||
| 3 |
| a2 |
| c |
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x0,y0)处的切线方程为:x0x+y0y=r2”.由上述结论类比得到:“过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
(2)利用(1)中的结论证明直线AB恒过定点(2
| 2 |
(3)当点M的纵坐标为1时,求△ABM的面积. 查看习题详情和答案>>
已知椭圆C: ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率 .过直线l:
.过直线l: 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x,y)处的切线方程为:xx+yy=r2”.由上述结论类比得到:“过椭圆 (a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).
(2)利用(1)中的结论证明直线AB恒过定点( );
);
(3)当点M的纵坐标为1时,求△ABM的面积.
查看习题详情和答案>>
 ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率 .过直线l:
.过直线l: 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x,y)处的切线方程为:xx+yy=r2”.由上述结论类比得到:“过椭圆
 (a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).(2)利用(1)中的结论证明直线AB恒过定点(
 );
);(3)当点M的纵坐标为1时,求△ABM的面积.
查看习题详情和答案>>
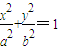 ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2,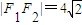 ,离心率
,离心率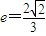 .过直线l:
.过直线l: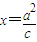 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.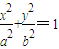 (a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).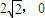 );
);