摘要：如图.AB是⊙O的直径.BD是⊙O的弦.延长BD到点C.使DC=BD.连结AC.过点D作DE⊥AC.垂足为E. (1)求证:AB=AC, (2)求证:DE为⊙O的切线, (3)若⊙O的半径为5,∠BAC=60°,求DE的长. (2008年施恩自治州,本题知识点有圆的直径定义.圆的切线判别.等边三角形概念.三角函数等,考查学生分析问题综合运用所学知识解决问题的能力) 答案:(1)证明:连接AD ∵AB是⊙O的直径 ∴∠ADB=90° 又BD=CD ∴AD是BC的垂直平分线 ∴AB=AC (2)连接OD ∵点O.D分别是AB.BC的中点 ∴OD∥AC 又DE⊥AC ∴OD⊥DE ∴DE为⊙O的切线 (3)由AB=AC, ∠BAC=60°知∆ABC是等边三角形 ∵⊙O的半径为5 ∴AB=BC=10, CD=BC=5 又∠C=60° ∴DE=CD·sin60°=
网址：http://m.1010jiajiao.com/timu_id_4418735[举报]
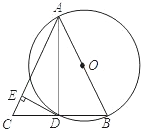如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：AB=AC；
（2）求证：DE为⊙O的切线；
（3）若⊙O的半径为5，∠BAC=60°，求DE的长． 查看习题详情和答案>>
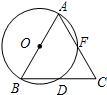24、如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC交⊙O于点F．（1）AB与AC的大小有什么关系？为什么？
（2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由．
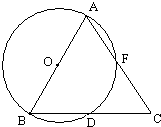22、如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC交⊙O与点F．（1）AB与AC的大小有什么关系？为什么？
（2）按角的大小分类，请你判断△ABC属于哪一类三角形．
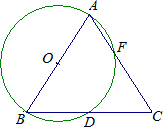如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC交⊙O于点F．（1）AB与AC的大小有什么关系？为什么？
（2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由．
小明按下面的方法作出了∠MON的平分线：
①反向延长射线OM；
②以点O为圆心，任意长为半径作圆，分别交∠MON的两边于点A、B，交射线OM的反向延长
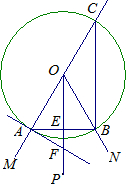线于点C；③连接CB；
④以O为顶点，OA为一边作∠AOP=∠OCB．
（1）根据上述作图，射线OP是∠MON的平分线吗？并说明理由．
（2）若过点A作⊙O的切线交射线OP于点F，连接AB交OP于点E，当∠MON=60°、OF=10时，求AE的长． 查看习题详情和答案>>
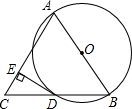如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．