摘要:一是错题集:从错误中学习到正确的知识.是学习的重要而有效的方法之一.建立一个错题集.平时经常看看.确定掌握好的.今后不再犯的错解.就做出标记.建立这样的一个错题集.到邻近高考的时候常犯的错误也就不多了.剩下的一些常犯错误就是高考冲刺时查漏补缺的主要目标.才能真正提高高考冲刺的效率.为高考的成功奠定必要的基石;二是试卷详解集:在高三接近一年的复习中.各类考试至少也有20次.每次考试后的试卷除了订正错误.认真总结考试的得失外.还要把整个试卷包括选择填空题做出详细的解答.标出解答题的评分标准.把这些试卷妥善保管.这些试卷在最后的高考冲刺阶段是考生最重要的.最贴合考生实际的全面回顾高考考点和查漏补缺的宝贵资料.是老师所不能代替的.
网址:http://m.1010jiajiao.com/timu_id_4417724[举报]
某地区教研部门要对高三期中数学练习进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从所有试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计这个地区高三学生该题的平均分;
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率. 查看习题详情和答案>>
| 第一空得分情况 | 第二空得分情况 | |||||
| 得分 | 0 | 3 | 得分 | 0 | 2 | |
| 人数 | 198 | 802 | 人数 | 698 | 302 | |
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率. 查看习题详情和答案>>
某地区教研部门要对高三期中数学练习进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从所有试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计这个地区高三学生该题的平均分;
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
查看习题详情和答案>>
| 第一空得分情况 | 第二空得分情况 | |||||
| 得分 | 0 | 3 | 得分 | 0 | 2 | |
| 人数 | 198 | 802 | 人数 | 698 | 302 | |
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
某地区教研部门要对高三数学期中考试进行调研,考察试卷中某道填空题的得分情况。已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分。第一空答对与否与第二空答对与否是相互独立的,从所有试卷中随机抽取1000份,其中该题的得分组成容量为1000的样本,统计结果如下表:
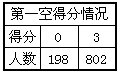

(1)求样本试卷中该题的平均得分,并据此估计整个地区中该题的平均得分;
(2)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,对于该填空题,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率,试求该同学第一空得分不低于第二空得分的概率。
查看习题详情和答案>>
(2)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,对于该填空题,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率,试求该同学第一空得分不低于第二空得分的概率。
某地区教研部门要对高三期中数学练习进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从所有试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计这个地区高三学生该题的平均分;
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
查看习题详情和答案>>
| 第一空得分情况 | 第二空得分情况 | |||||
| 得分 | 3 | 得分 | 2 | |||
| 人数 | 198 | 802 | 人数 | 698 | 302 | |
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
查看习题详情和答案>>
某地区教研部门要对高三期中数学练习进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从所有试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计这个地区高三学生该题的平均分;
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
查看习题详情和答案>>
| 第一空得分情况 | 第二空得分情况 | |||||
| 得分 | 3 | 得分 | 2 | |||
| 人数 | 198 | 802 | 人数 | 698 | 302 | |
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
查看习题详情和答案>>