摘要:22.本题共有3个小题.第1小题满分3分.第2小题满分7分.第3小题满分8分) 由函数y=f(x)确定数列{an}.an=f的反函数y=f –1(x)能确定数列{bn}.bn= f –1(n).若对于任意nÎN*.都有bn=an.则称数列{bn}是数列{an}的“自反数列 . =确定数列{an}的自反数列为{bn}.求an, 条件下.记为正数数列{xn}的调和平均数.若dn=.Sn为数列{dn}的前n项之和.Hn为数列{Sn}的调和平均数.求, (3)已知正数数列{cn}的前n项之和 求Tn表达式.
网址:http://m.1010jiajiao.com/timu_id_4417531[举报]
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知集合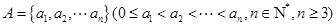 具有性质
具有性质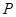 :对任意
:对任意 ,
,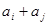 与
与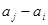 至少一个属于
至少一个属于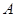 .
.
(1)分别判断集合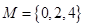 与
与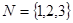 是否具有性质
是否具有性质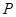 ,并说明理由;
,并说明理由;
(2)①求证: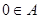 ;
;
②求证: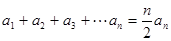 ;
;
(3)研究当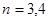 和
和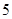 时,集合
时,集合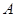 中的数列
中的数列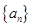 是否一定成等差数列.
是否一定成等差数列.
查看习题详情和答案>>
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数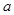 的值;
的值;
(3)在(2)的条件下,是否存在实数 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为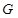 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数 的值;
的值;
(3)在(2)的条件下,是否存在实数 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
对定义在
 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为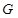 函数.
函数.① 对任意的
 ,总有
,总有 ;
;② 当
 时,总有
时,总有 成立.
成立.已知函数
 与
与 是定义在
是定义在 上的函数.
上的函数.(1)试问函数
 是否为
是否为 函数?并说明理由;
函数?并说明理由;(2)若函数
 是
是 函数,求实数
函数,求实数 的值;
的值;(3)在(2)的条件下,是否存在实数
 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.