摘要:平面向量的数量积 (1)定义:已知两个非零向量和.它们的夹角为θ.则数量||||cosθ叫做与的数量积.记作·.即·=||||cosθ 规定:零向量与任一向量的数量积是0. (2)几何意义:数量积·等于的长度||与在的方向上的投影||cosθ的乘积. (3)性质:设.都是非零向量.是与方向相同的单位向量.θ是与的夹角.则·=·=||cosθ .⊥·=0 当与同向时.·=|||| 当与反向时.·=-|||| 特别地.·=||2或||= cosθ= |·|≤|||| (4)运算律: ·=· (λ)·=λ(·)=·(λ) (+)·=·+· (5)平面向量垂直的坐标表示的充要条件: 设=(x1 ,y1), = (x2,y2).则 ·=||·||cos90°=0 x1x2+y1y2=0
网址:http://m.1010jiajiao.com/timu_id_4416772[举报]
将平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
(1)
•
=
•
;
(2)(
•
)•
=
•(
•
);
(3)
•(
+
)=
•
+
•
;
(4)由
•
=
•
(
≠
)可得
=
.
以上通过类比得到的结论正确的有( )
(1)
| a |
| b |
| b |
| a |
(2)(
| a |
| b |
| c |
| a |
| b |
| c |
(3)
| a |
| b |
| c |
| a |
| b |
| a |
| c |
(4)由
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
以上通过类比得到的结论正确的有( )
查看习题详情和答案>>
关于平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
①
•
=
•
;②(
•
)•
=
•(
•
);③
•(
+
)=
•
+
•
;
④|
•
|=|
|•|
|;⑤由
•
=
•
(
≠
),可得
=
.
以上通过类比得到的结论正确的有( )
①
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
④|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| c |
| a |
| 0 |
| b |
| c |
以上通过类比得到的结论正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
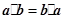 ;②
;②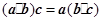 ;③
;③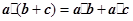 ;
;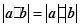 ;⑤由
;⑤由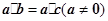 可得
可得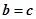 .
. ;
;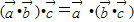 ;
;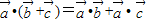 ;
; 可得
可得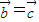 .
.