摘要:解:(Ⅰ)当时..,---2分 对于[1.e].有.∴在区间[1.e]上为增函数.-3分 ∴..-----------5分 (Ⅱ)令. 则的定义域为.----6分 在区间上函数的图象恒在直线下方等价于在区间上恒成立. ∵ ① 若.令.得极值点.. 当.即时.在(.+∞)上有. 此时在区间(.+∞)上是增函数.并且在该区间上有 ∈(.+∞).不合题意,---------------8分 当.即时.同理可知.在区间上.有 ∈(.+∞).也不合题意,---------------9分 ② 若.则有.此时在区间上恒有. 从而在区间上是减函数,--------------10分 要使在此区间上恒成立.只须满足. 由此求得的范围是[.]. 综合①②可知.当∈[.]时. 函数的图象恒在直线下方. ------12分
网址:http://m.1010jiajiao.com/timu_id_4415541[举报]
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明:
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f(x)在[1,2]上是减函数,的导函数恒小于等于零,然后分离参数求解得到a的取值范围。第二问中,
假设存在实数a,使 有最小值3,利用
有最小值3,利用 ,对a分类讨论,进行求解得到a的值。
,对a分类讨论,进行求解得到a的值。
第三问中,
因为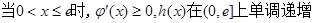 ,这样利用单调性证明得到不等式成立。
,这样利用单调性证明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)见解析
查看习题详情和答案>>