摘要: (1)证明:∵AE∥BD, ∴∠E=∠BDC ∵DB平分∠ADC ∴∠ADC=2∠BDC 又∵∠C=2∠E ∴∠ADC=∠BCD ∴梯形ABCD是等腰梯形 问.得∠C=2∠E=2∠BDC=60°.且BC=AD=5 ∵ 在△BCD中.∠C=60°, ∠BDC=30° ∴∠DBC=90° ∴DC=2BC=10
网址:http://m.1010jiajiao.com/timu_id_4412381[举报]
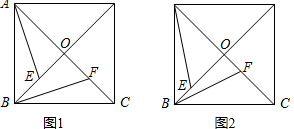
已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,
(1)如果动点E、F满足BE=CF(如图1):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)如果动点E、F满足BE=OF(如图2),问当AE⊥BF时,点E在什么位置,并证明你的结论.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)如果动点E、F满足BE=CF(如图1):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)如果动点E、F满足BE=OF(如图2),问当AE⊥BF时,点E在什么位置,并证明你的结论.
 查看习题详情和答案>>
查看习题详情和答案>>
 20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C
20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C证明:∵AE∥BC
已知
∴∠1=
∠B(两直线平行,同位角相等)
∠2=
∠C(两直线平行,内错角相等)
又∵AE平分∠CAD
∴∠1=∠2
角平分线的定义
∴∠
B
=∠C
.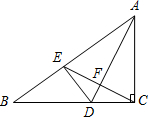 如图,△ABC中,∠C=90°,AD是角平分线,DE⊥AB,垂足是E.
如图,△ABC中,∠C=90°,AD是角平分线,DE⊥AB,垂足是E.  如图,A、B、C、D在同一直线上,AB=CD,AE∥BF,AE=BF.请补充完整证明“CE∥DF”的推理过程.
如图,A、B、C、D在同一直线上,AB=CD,AE∥BF,AE=BF.请补充完整证明“CE∥DF”的推理过程.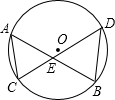 如图,⊙O的两条弦AB、CD相交于点E,连接AC、BD,试证明:AE•BE=CE•DE.
如图,⊙O的两条弦AB、CD相交于点E,连接AC、BD,试证明:AE•BE=CE•DE.