题目内容
 20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C
20、如图,AE∥BC,AE平分∠CAD,试说明∠B=∠C证明:∵AE∥BC
已知
∴∠1=
∠B(两直线平行,同位角相等)
∠2=
∠C(两直线平行,内错角相等)
又∵AE平分∠CAD
∴∠1=∠2
角平分线的定义
∴∠
B
=∠C
.分析:由AE∥BC,根据两直线平行,同位角相等与两直线平行,内错角相等即可求得∠1=∠B,∠2=∠C,又由AE平分∠CAD,即可求得∠B=∠C.
解答:证明:∵AE∥BC( 已知 )
∴∠1=∠B ( 两直线平行,同位角相等 )
∠2=∠C ( 两直线平行,内错角相等 )
又∵AE平分∠CAD
∴∠1=∠2( 角平分线的定义 )
∴∠B=∠C ( 等量代换 )
故答案为:已知;∠B,两直线平行,同位角相等;∠C,两直线平行,内错角相等;角平分线的定义;B,C.
∴∠1=∠B ( 两直线平行,同位角相等 )
∠2=∠C ( 两直线平行,内错角相等 )
又∵AE平分∠CAD
∴∠1=∠2( 角平分线的定义 )
∴∠B=∠C ( 等量代换 )
故答案为:已知;∠B,两直线平行,同位角相等;∠C,两直线平行,内错角相等;角平分线的定义;B,C.
点评:此题考查了平行线的性质.解题的关键是注意掌握两直线平行,同位角相等与两直线平行,内错角相等定理的应用.

练习册系列答案
相关题目
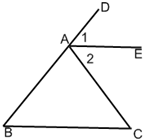 27、如图,AE∥BC,AE平分∠CAD,观察图中∠B与∠C有什么关系?并说明理由.
27、如图,AE∥BC,AE平分∠CAD,观察图中∠B与∠C有什么关系?并说明理由. 26、已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
26、已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.