94、小红和小兵一起做一道题：依据下面条件求等腰三角形的三个内角的度数．（1）一个角为另一个角的2倍；（2）两角之差为30度．
小兵做出了以下解答过程：
（1）设等腰三角形的顶角为x°，则底角为2x，由题意得x+2x+2x=180°，解得x=36，所以2x=72，所以这个等腰三角形的三个内角为36°，72°，72度．
小红做出了以下解答过程：
（2）设等腰三角形的顶角为x°，则底角为（x+30°），由题意得x+2（x+30）=180，解得x=40，所以x+30=70，所以这个等腰三角形的三个内角度数为40°，70°，70度．
小红看了解答以后说：“小兵你错了”．
亲爱的同学，你说他们的答案到底谁错了？错在哪里呢？

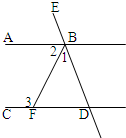如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF．
下面给出证法1．
证法1：∠1、∠2、∠3的度数分别为x，2x，3x，
∵AB∥CD，∴2x+3x=180°，解得x=36°
∴∠1=36°，∠2=72°，∠3=108°，
∵∠EBD=180°，∴∠EBA=72°，
∴BA平分∠EBF
请阅读证法1后，找出与证法1不同的证法2，并写出证明过程．

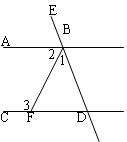
如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF，下面给出证法1    
证法1：∠1、∠2、∠3的度数分别为x，2x，3x
 ∵AB∥CD，
∴2x+3x=180°，
解得x=36°  
∴∠1=36°，∠2=72°，∠3=108°  
∵∠EBD=180°，
∴∠EBA=72°  
∴BA平分∠EBF    
请阅读证法1后，找出与证法1不同的证法2，并写出证明过程。

小红和小兵一起做一道题：依据下面条件求等腰三角形的三个内角的度数．（1）一个角为另一个角的2倍；（2）两角之差为30度．
小兵做出了以下解答过程：
（1）设等腰三角形的顶角为x°，则底角为2x，由题意得x+2x+2x=180°，解得x=36，所以2x=72，所以这个等腰三角形的三个内角为36°，72°，72度．
小红做出了以下解答过程：
（2）设等腰三角形的顶角为x°，则底角为（x+30°），由题意得x+2（x+30）=180，解得x=40，所以x+30=70，所以这个等腰三角形的三个内角度数为40°，70°，70度．
小红看了解答以后说：“小兵你错了”．
亲爱的同学，你说他们的答案到底谁错了？错在哪里呢？